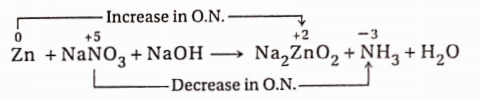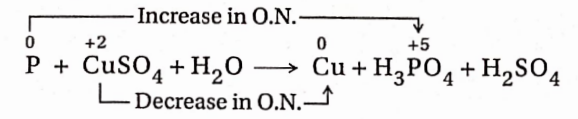Sainavle

Heat Of Reaction

Heat Of Reaction Definition

The amount of heat absorbed or evolved in a reaction when the stoichiometric number of moles of reactions indicated by the balanced chemical equation, is completely converted into products at given conditions is called the heat of reaction at that conditions.

At a particular temperature, the heat of a reaction depends on the conditions under which a reaction is occurring. Generally, chemical reactions are carried out either at constant pressure or at constant volume. Accordingly, the heat of reaction is of two types, namely Heat of reaction at constant volume and heat of reaction at constant pressure.

The heat of reaction at constant volume

The amount of heat absorbed or evolved in a reaction when the stoichiometric number of moles of reactants, indicated by the balanced chemical equation of the reaction, is completely converted into products at a fixed temperature and volume is called the heat of reaction at constant volume.

Explanation: Let us consider a chemical reaction that is occurring at constant temperature and volume.

⇒ \(a A+b B \rightarrow c C+d D\)

According to die first law of thermodynamics, if a reaction occurs at constant volume then the heat change (qv) is equal to the change in internal energy (AU) ofthe system (provided only pressure-volume work is performed), qv= ΔU

Therefore, for the reaction

⇒ \(q_V=\Delta U=\Sigma U_{\text {products }}-\Sigma U_{\text {reactants }}=\Sigma U_P-\Sigma U_R\)

where ΣUp = total internal energy of products and I UR = total internal energy of reactants.

∴ \(q_V=\Sigma U_p-\Sigma U_R=\left(c \bar{U}_C+d \bar{U}_D\right)-\left(a \bar{U}_A+b \bar{U}_B\right)\)

Where \(\bar{U}_A, \bar{U}_B, \bar{U}_C \text { and } \bar{U}_D\) die molar internal energies of A. B. Cand D, respectively. Thus, the heat of reaction for a reaction at constant temperature and volume is the difference between the total internal energy of tire products and the total internal energy of the reactants.

Example:

⇒  \(\mathrm{CH}_4(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

For the above reaction, the heat of the reaction at a constant volume:

⇒ \(q_V=\left[\bar{U}\left(\mathrm{CO}_2, g\right)+2 \bar{U}\left(\mathrm{H}_2 \mathrm{O}, l\right)\right]-\left[\bar{U}\left(\mathrm{CH}_4, g\right)+2 \bar{U}\left(\mathrm{O}_2, g\right)\right]\)

Where

⇒ \(\bar{U}\left(\mathrm{CO}_2, \mathrm{~g}\right), \bar{U}\left(\mathrm{H}_2 \mathrm{O}, l\right), \bar{U}\left(\mathrm{CH}_4, g\right) \text { and } \bar{U}\left(\mathrm{O}_2, g\right)\)

Are die molar internal energies of CO,(g), H₂O(I), CH₄(g) respectively.

Heat of reaction at constant pressure:

The amount of heat absorbed or evolved in a reaction when the stoichiometric number of moles of reactants, indicated by a balanced chemical equation of the reaction, is completely converted into products at constant pressure, and temperature is called the heat of reaction at constant pressure.

The heat of reaction at constant pressure Explanation:

Let us consider a reaction that is occurring at constant temperature and pressure: aA + bB →+ cC + dD. According to the first law of thermodynamics, if a reaction occurs at constant pressure, then the heat change in the reaction is equal to the change in enthalpy of the system (provided only pressure-volume work is performed). Thus, qp = ΔH. Therefore, for the reaction,

⇒ \(q_P=\Delta H=\Sigma H_{\text {products }}-\Sigma H_{\text {reactants }}=\Sigma H_P-\Sigma H_R \text { ; }\)

where Hp = total enthalpy ofthe products and HR = total enthalpy of the reactants

∴ \(q_P=\Sigma H_P-\Sigma H_R=\left(c \bar{H}_C+d \bar{H}_D\right)-\left(a \bar{H}_A+b \bar{H}_B\right)\)

where, \(\bar{H}_A, \bar{H}_B, \bar{H}_C \text { and } \bar{H}_D\) are the molar enthalpies of A, B, C, and D, respectively.

Thus, for a reaction, the heat of the reaction at constant temperature and pressure is equal to the difference between the total enthalpy of products and the total enthalpy of reactants.

Example:

For the Reaction, \(2 \mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(l)\) the heat ofreaction at constant pressure is given by;

⇒ \(q_P=2 \bar{H}\left(\mathrm{H}_2 \mathrm{O}, l\right)-\left[2 \bar{H}\left(\mathrm{H}_2, \mathrm{~g}\right)+\bar{H}\left(\mathrm{O}_2, \mathrm{~g}\right)\right]\)

Where \(\bar{H}\left(\mathrm{H}_2 \mathrm{O}, l\right), \bar{H}\left(\mathrm{H}_2, \mathrm{~g}\right) \text { and } \bar{H}\left(\mathrm{O}_2, \mathrm{~g}\right)\) are the molar enthalpies of H₂O(g) , H₂(g) and O₂(g) , respectively.

Relation between heat of reaction at constant volume [q_v) and heat of reaction at constant pressure (q_p)

If a reaction is carried out at a fixed pressure than the heat of the reaction, qp = change in enthalpy in the reaction, ΔH. …………………(1)

If the reaction is carried out at constant volume then the heat of the reaction, qv = change in internal energy in the reaction, ΔU …………………(2)

If the changes in internal energy and volume in a reaction occurring at constant pressure are AUp and AV, respectively, then according to the relation H = U + PV

⇒ \(\Delta H=\Delta U_P+\Delta(P V)=\Delta U_P+P \Delta V\)

[As pressure (P) is constant, Δ(PV) = PΔV

∴ \(q_P=\Delta H=\Delta U_P+P \Delta V\) …………………(3)

since qp = ΔH

Subtracting equation [2] from [3], we obtain

∴ \(q_P-q_V=\Delta U_P+P \Delta V-\Delta U=\left(\Delta U_P-\Delta U\right)+P \Delta V\)

At a particular temperature, the difference between AUp (change in internal energy at constant pressure) and AU (change in internal energy at constant volume) is very small. Therefore, it is considered that

⇒ \(\Delta U_P \approx \Delta U.\)

Since q_p -q_v = PΔV

Or, ΔH-ΔU = PΔV ………………………….(4)

In the case of solids and liquids:

For reactions involving only solids and liquids, the change in volume (ΔV) of the reaction system is negligibly small. So, in such reactions, the heat of the reaction at constant pressure (qp or ΔH) becomes equal to the heat of the reaction at constant volume (qV or ΔU).

In the case of gases:

For a reaction involving gaseous substances

Example:

⇒  \(A(g)+B(g) \rightarrow C(g) \text { or } A(g)+B(g) \rightarrow C(I)\),

Or \(A(s) \rightarrow B(s)+C(g)\), etc.]

The change in volume (Δ V) of the reaction system may be sufficiently high. We can determine the value of PΔV as illustrated below

Let us consider a gaseous reaction that occurs at constant pressure (P) and temperature (T).

Suppose, n₁ and V₁ are the total number of moles and the total volume of the reactant gases, respectively, and n₂ and IA, are the Here, total number of moles and the total volume of the product gases respectively. If the gases are assumed to behave ideally, then for gaseous reactants PV₁ = n₁RT., and gaseous products PV₂ = n₂RT.

∴ \(P\left(V_2-V_1\right)=\left(n_2-n_1\right) R T \text { or, } P \Delta V=\Delta n R T\)

Substituting ΔnRT for PΔV into equation (4) we obtain

⇒  \(q_p-q_V=\Delta n R T \text { and } \Delta H-\Delta U=\Delta n R T\)

∴ \(\left[\boldsymbol{q}_p=\boldsymbol{q}_V+\Delta n \| T\right] \text { and }[\Delta I=\Delta U+\Delta n \ RT] \cdot \cdot \cdot \cdot \cdot [5]\)

Using equation (5), ΔH (or qp) can be calculated from the known value of U (or Δv), and ΔU (or qV) can be calculated from the known value of AII (or ΔyU). If

Δn=0; ΔH=ΔU;Δn>0,ΔH>ΔU;Δn>0,ΔH<ΔU.

Comparison between the values of ΔH and ΔU for gaseous reaction having different Δn values:

Standard State And Standard Reaction Enthalpy

Enthalpy change in a reaction depends on the conditions of temperature, pressure, and physical states of the reactants and products. To compare enthalpies of different reactions, we define a set of conditions called standard state, at which the values of AH for different reactions are calculated.

Standard State:

The standard state ofa substance is defined as the most stable and purest state of that substance at the temperature of interest and atm pressure. In the definition of the standard state, temperature is not specified like pressure (1 atm). If the temperature is not mentioned, then 25 °C (298.15 K) is taken as a reference temperature. However, this does not mean 25 °C is the standard temperature. A pure substance can have different standard states depending on the temperature of interest, but in each of these states, the pressure is always 1 atm.

Examples:

• The standard state of liquid water at a particular temperature means H₂O(l) at that temperature and 1 atm pressure.
• The standard state of ice at a particular temperature means pure H₂O(s) at that temperature and atm pressure.
• The standard state of liquid ethanol at 25 °C means C₂H₅OH(l) at 25 °C and 1 atm pressure.

Standard enthalpy of reaction:

The standard enthalpy change of a reaction is defined as the enthalpy change that occurs when the stoichiometric number of moles of reactants, indicated by the balanced chemical equation of the reaction, is completely converted into products at a particular temperature and l atm (i.e., at the standard state).

The standard enthalpy of reaction at a particular temperature ( T K) is denoted by \(\Delta H_T^0\). The superscript ‘0’ indicates the standard state, and the subscript T indicates the temperature in the Kelvin scale.

Explanation:

⇒ \(\mathrm{C}_3 \mathrm{H}_8(\mathrm{~g})+5 \mathrm{O}_2(\mathrm{~g}) \rightarrow 3 \mathrm{CO}_2(\mathrm{~g})+4 \mathrm{H}_2 \mathrm{O}(l)\)

For this reaction \(\Delta H_{2 \mathrm{qg}}^0=-2220 \mathrm{~kJ}\) indicating that at.

• 298 K temperature and atm pressure, if lmol of propane (C₃H₈) and mol of O₂ react completely to form 3 mol of CO, and 4 mol of water at the same temperature and pressure (i.e, 29S K and atm respectively), then 2220 kj of heat will be evolved.
• Alternatively, it can be said that at 298K temperature and 1 atm pressure, the change in enthalpy for the following reaction is =-2220 kJ.

Factors affecting the reaction enthalpy

1. Physical states of reactants and products:

During the change of physical states of a substance (like solid, solid→ liquid, liquid→ vapor, etc.) heat is either absorbed or evolved. Thus, the value of the heat of the reaction or enthalpy of the reaction depends upon the physical states ofthe reactants and products. For example, in the following two reactions, due to the different physical states ofthe products,

The values ofthe heat of the reaction are different:

⇒ \(2 \mathrm{H}_2(g)+\mathrm{O}_2(g) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(l) ; \Delta H=-571.6 \mathrm{~kJ}\)

⇒ \(2 \mathrm{H}_2(g)+\mathrm{O}_2(g) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(g) ; \Delta H=-483.6 \mathrm{~kJ}\)

2. The condition under which the reaction is conducted:

At a particular temperature, a chemical reaction can be conducted either at constant pressure or at constant volume. If a reaction occurs at constant pressure, then the heat of reaction (q_p)

⇒ \(=H_{\text {product }}-H_{\text {reactant }}=\Delta H\)

Occurs at constant volume, then the heat of reaction (q_p) — The relation between ΔH and ΔH is ΔH = ΔH + PΔV The quantity PAV indicates pressure-volume work.

• So, the difference between ΔH and AH is equal to the pressure-volume work involved during the reaction.
• If the volume of the reacting system remains fixed (ΔV = 0), then pressure-volume work = 0 and ΔH = ΔH.
• If the volume ofthe reacting system changes (ΔV=0), then, the pressure-volume work, PΔV≠0 and ΔH≠ΔU.

3. Allotropic forms of the reacting elements:

As the different allotropic forms have different enthalpies, the value of reaction enthalpy depends upon the allotropic forms of the reactants.

For example, the enthalpies of the reaction are different for the oxidation of graphite and diamond (two allotropic forms of carbon)

⇒ \(\mathrm{C}(\text { graphitè, } s)+\mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})\)

ΔH=-393.5 kJ

⇒\(\mathrm{C}(\text { diamond, } s)+\mathrm{O}_2(g) \rightarrow \mathrm{CO}_2(g)\)

Δ H =-395.4 kJ

4. Amount of the reactants:

As enthalpy is an extensive property, the magnitude of enthalpy change in a reaction (ΔH) is proportional to the amount of reactants undergoing the reaction.

For example, in the reactions given below, the magnitude of ΔH (reaction enthalpy) for reaction (1) is twice that for the reaction (1). This is because the total number of moles of reactants in the reaction (2) is twice as many as that in the reaction (1).

⇒ \(\mathrm{H}_2(g)+\frac{1}{2} \mathrm{O}_2(g) \rightarrow \mathrm{H}_2 \mathrm{O}(l), \Delta H=-285.8 \mathrm{~kJ}\) ……………………………..(1)

⇒ \(2 \mathrm{H}_2(g)+\mathrm{O}_2(g) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(l), \Delta H=-571.6 \mathrm{~kJ}\) ……………………………..(2)

5. Temperature:

Temperature has a significant effect on the reaction enthalpy of a reaction. The extent of temperature dependence of the reaction enthalpy depends on the nature of the reaction.

Heat Of Reaction Numerical Examples

Question 1. The value of ΔH for the given reaction at 298K is — 282.85 kj. mol^-1. Calculate the change in internal energy: \(\mathrm{CO}(g)+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})\)
Answer:

We know, ΔH = ΔH + ΔnRT where, Δn = (total number of moles of the gaseous products) — (total number of moles of the gaseous reactants)

For the given reaction, ,\(\Delta n=1-\left(1+\frac{1}{2}\right)=-\frac{1}{2}\)

As per given data, ΔH = -282.85 kj-mol^-1 & T = 298 K

∴ \(-282.85=\Delta U+\left[\left(-\frac{1}{2}\right) \times 8.314 \times 10^{-3} \times 298\right]\)

∴ \(\Delta U=-281.61 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}\)

Question 2. The bond energy of a diatomic molecule IN given as the change in internal energy due to dissociation of that molecule. Calculate the bond energy of O₂. Given: \(\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{O}(\mathrm{g}) ; \Delta H=498.3 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}, T=298 \mathrm{~K}\)
Answer:

In the dissociation reaction of O₂ molecules, Δn = 2-1 = 1.

We know, ΔH = ΔU + ΔnRT

As given, ΔH = 498.3 kj.mol^-1 , T = 298 K

∴ \(498.3=\Delta U+\left(1 \times 8.314 \times 10^{-3} \times 298\right)\)

or, ΔU= 495.8J

∴ Bond energy of O₂ molecule = 495.8 kj.mol^-1

Question 3. Calculate the values of ΔH and ΔH in the vaporization of 90 g of water at 100°C and 1 atm pressure. The latent heat of vaporization of water at the same temperature and pressure = 540 cal g^-1.
Answer:

⇒ \(90 \mathrm{~g} \text { of water }=\frac{90}{18}=5 \mathrm{~mol} \text { of water. }\)

Vaporisation of water:

⇒ \(\mathrm{H}_2 \mathrm{O}(l) \rightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

Therefore, in the vaporization of1 mol of water, Δn = +1.

Hence, for the vaporization of 5 mol water, Δn = +5.

So, the amount of heat required to vaporize 90 g (5 mol) of water =540 x 90 = 48600 cal.

As the vaporization process occurs at constant pressure (1 atm), the heat absorbed = enthalpy change.

∴ The change in enthalpy in the vaporization of 90g of water, ΔH = 48600 cal

∴ The change in internal energy in the vaporization of 90gofwater, ΔH = ΔH-ΔnRT

= 48600- 5 × 1.987 × (273 + 100) = 44894.24 cal .

Question 4. Assuming the reactant and product gases obey its ideal gas law, calculate the change in internal energy (AE) at 27°C for the given reaction:
Answer:

⇒ \(\mathrm{C}_2 \mathrm{H}_4(\mathrm{~g})+3 \mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(l) ;\)

In tlui rimdlon, Δn= 2-1=1.

We know, ΔH = ΔU+ΔuRT

As given, ΔH = 498.3 kj. mol^-1 , T = 298 K

∴ 498.3 = ΔH + (1 × 8.314 × 10-3 × 298) or, ΔH = 495.8 kJ

The bond energy of the O₂ molecule = 495.8 kj.mol^-1

In the reaction , Δn =2- (1 + 3)= -2

we know ΔH+ ΔnRT

Or, 337= ΔU-2 × 1.987 × 10^-3 × 300

Or, ΔU =-335.8kcal

Balancing Of Chemical Equations Involving Redox Reactions

Redox reaction can be balanced with the help of two methods. These are the

1. Ion-electron method
2. Oxidation number method.

Ion-electron method

Jade and Lamer in 1927 introduced this method. In the ion-electron method, only the molecules and ions which participate in the chemical reaction are shown.

In balancing redox reactions by this method the following steps are followed: 

• The reaction is written in ionic form.
• The reaction is divided into two half-reactions with the help of ions and electrons. One half-reaction is for oxidation reaction and the other half-reaction is for reduction reaction.
• While writing the oxidation reaction, the reducing agent and the oxidised substance are written respectively on the left and right of an arrow signing are written respectively on the left and right of the arrow sign
• To denote the loss of electrons in oxidation half-reaction, the number of electrons (s) is written on the right of the arrow sign (→). While writing the reduction half-reaction, the number of electrons (s) gained is written on the left arrow sign ( →).

Thus, the oxidation half-reaction is:

Reducing agent – Oxidised substance +ne [where n = no. of electron (s) lost in oxidation reaction] Thus reduction half-reaction is Oxidising agent + ne Reduced substance [where n = no. of electron(s) gained reduction reaction] 2Cr³⁺

Then each half-reaction is balanced according to the following steps:

In each of the half-reactions, the number of atoms other than H and O -atoms on both sides ofthe arrow sign is balanced.

If a reaction takes place in an acidic medium, for balancing the number of H and O-atoms on both sides of the arrow sign, H₂O or H⁺ is used. First, oxygen atoms are balanced by adding H₂O molecules to the side that needs O-atoms.

Then to balance the number of H-atoms, two H⁺ ions (2H⁺) for each molecule of water are added to the opposite side (i.e., the side deficient in hydrogen atoms) of the reaction occurs in an alkaline medium, for balancing the H and O -atoms, H₂O or OH^– ion is used.

• Each excess oxygen atom on one side of the arrow sign is balanced by adding one water molecule to the same side and two ions to the other side.
• If the hydrogen atom is still not balanced, it is then balanced by adding one OH^– for every excess hydrogen atom on the side of the hydrogen atoms and one water molecule on the other side of the arrow sign in a half-reaction, both H⁺ and OH^– ions cannot participate.
• The charge on both sides of each half-reaction is balanced. This is done by adding an electron to that side which is a deficient negative charge.
• To equalise the number of electrons of the two half-reactions, any one of the reactions or both reactions should be multiplied by suitable integers.
• Now, the two half-reactions thus obtained are added. Cancelling the common term(s) on both sides, the balanced equation is obtained.

Examples:

1. In the presence of H₂SO₄, potassium dichromate (K₂Cr₂O₂) and ferrous sulphate (FeSO₄) react together to produce ferric sulphate [Fe₂(SO₄)₃] and chromic sulphate [Cr₂(SO₄)₃].

Reaction:

K₂Cr₂O₇ + FeSO₄ + H₂SO₄→ K₂SO₄ + Cr₂(SO₄)₃ + Fe₂(SO₄)₃ + H₂O

The reaction can be expressed in ionic form as:

Cr³⁺ + Fe³⁺ + H₂O

Oxidation half-reaction: Fe²⁺→Fe³⁺+ e ……………………(1)

Reduction half-reaction: Cr₂O₇^2-+ Cr³⁺ ……………………(2)

1. Balancing the Cr -atom: Cr₂O₇^2-– Cr³+ 7H₂O

2.To equalise the number of O -atoms on both sides, 7 water molecules are to be added to the right side. 2Cr³⁺ + 7H₂O

⇒ \(\mathrm{Cr}_2 \mathrm{O}_7^{2-} \longrightarrow 2 \mathrm{Cr}^{3+}+7 \mathrm{H}_2 \mathrm{O}\)

∴ One water molecule is required for each O-atom.

3. To balance H-atoms on both sides, 14H+ ions are to be added to the left side.

⇒ \(\mathrm{Cr}_2 \mathrm{O}_7^{2-}+14 \mathrm{H}^{+} \longrightarrow 2 \mathrm{Cr}^{3+}+7 \mathrm{H}_2 \mathrm{O}\)

∴ 2H⁺ ions are required for each water molecule.

4. For equalising the charge on both sides, 6 electrons are to be added to the left side.

⇒ \(\mathrm{Cr}_7 \mathrm{O}_7^{2-}+14 \mathrm{H}^{+}+6 e \longrightarrow 2 \mathrm{Cr}^{3+}+7 \mathrm{H}_2 \mathrm{O}\)

Now, for balancing the number of electrons in oxidation and reduction half-reactions, the balanced oxidation half-reaction is multiplied by 6 and the balanced reduction half-reaction by 1. Then these two equations are added.

This balanced equation has been expressed in ionic form. This equation can be represented in molecular form as:

6FeSO₄ + K₂Cr₂O₇ + 7H₂SO₄ → 3Fe₂(SO₄)₃ + Cr₂(SO₄)₃+ K₂SO₄+ 7H₂O

∴ For 2H⁺ ions, one H₂SO₄ molecule is required

2. In presence of H₂SO₄, KMnO₄ and FeSO₄ react together to produce MnSO₄ and Fe₂(SO₄)₃.

Reaction: KMnO₄ + FeSO₄ + H₂SO₄ → K₂SO₄ + MnSO₄+ Fe₂(SO₄)3 + H₂O

The equation can be expressed in ionic form as:

MnO₄ + Fe²⁺ + H⁺→-Mn²⁺ + Fe³⁺ + H₂O

Oxidation half-reaction: Fe²⁺ — Fe³⁺ + e ………………………..(1)

Reduction half-reaction: MnO₄^– + 8H⁺ + 5e → Mn²⁺ + 4H₂O………………………..(2)

To balance the number of electrons lost in the oxidation half-reaction, the oxidation half-reaction is multiplied by 5 and then the two reactions are added.

As one Fe₂(SO₄)₃ molecule contains two Fe -atoms, the equation is multiplied by 2

10Fe²⁺ + MnO₄^– + 16H⁺ →10Fe³⁺ + 2Mn²⁺ + 8H₂O

This is the balanced equation in ionic form. This equation when expressed in molecular form becomes

10FeSO₄ + 2KMnO₄+ 8H₂SO₄ →  5Fe₂(SO₄)₃ + 2MnSO₄ + 8H₂O

Equalising the number of atoms of different elements and the sulphate radicals we get,

10FeSO₄+ 2KMnO₄ + 8H₂SO₄ → 5Fe₂(SO₄)₃ + 2MnSO₄ + K₂SO₄ + 8H₂O

This is a balanced equation of the given reaction in molecular form.

3. In the reaction between K₂Cr₂O₇ acidified with dilute H₂SO₄  and KI, Cr₂(SO₄)₃ and I₂ are formed.

K₂Cr₂O₇+KI + H₂SO₄ → K₂SO₄ + Cr₂(SO₄)₃ + I₂ + H₂O

The equation can be expressed in ionic form as— Cr₂O₇^2-+I^– + H⁺ — Cr³⁺ + I₂ + H₂O

Oxidation half-reaction: 2I^–→ I₂ + 2e……………..(1)

Reduction half-reaction: Cr₂O₇ ^2-+ I^–+14H⁺ + 6e — 2Cr³⁺ + 7H₂O ……………………….(2)

To balance the electrons, equation (1) is multiplied by 3 and added to equation (2). Thus the equation stands as—

This is the balanced equation of the reaction in ionic form. The above ionic reaction can be expressed in molecular form as follows

6KI + K₂Cr₂O₇ + 7H₂SO₄→3I₂ + Cr₂(SO₄)₃ + 7H₂O

Equalising the number of atoms of potassium and sulphate radical on the left and right sides, we have,

6KI + K₂Cr₂O₇+ 7H₂SO₄ → 3I₂ + Cr₂(SO₄)₃ + 4K₂SO₄ + 7H₂O

4. In the reaction between KMnO₄, acidified with dilute H₂SO₄ and oxalic acid (H₂C₂O₄), MnSO₄ and CO₂ were produced.

Reaction: KMnO₄ + H₂C₂O₄ + H₂SO₄ → K₂SO₄ + MnSO₄ + CO₂ + H₂O

Oxidation half-reaction: C₂O₄→  2CO₄^2-+ 2e ……………………..(1)

Reduction half-reaction: MnO₄^– +8H⁺+ 5e → Mn²⁺+ 4H₂O……………………..(2)

Now, multiplying equation (1) by 5 and equation (2) by 2 and then adding them, we get,

5C₂O₄ ^2-+ 2MnO₄ + 16H⁺+10CO₂ + 2Mn²⁺ + 8H₂O

This Is the balanced equation of the given reaction in molecular form.

5H₂C₂O₄ + 2KMnO₄+ 3H₂SO₄→ 10CO₂ + Mn²⁺ +8H₂O

Equalising the number of atoms of potassium and sulphate radical we get

5H₂C₂O₄ + 2KMnO₄ + 3H₂SO₄ → 10CO₂ + 2MnSO₄ + K₂SO₄ + 8H₂O

5. In NaOH solution, Zn reacts with NaNO₃ to yield Na₂ZnO₂, NH₃ and H₂O.

Reaction:

Zn + NaNO₃ + NaOH — Na₂ZnO₂ + NH₃ + H₂O The equation can be expressed in ionic form as—

Zn + NO^– + OH^–→ ZnO_2^– →+ NH₃ +H₂O

Oxidation half-reaction: Zn + 4OH^–→ ZnO₂^– + 2H₂O + 2C ……………………..(1)

Reduction half-reaction: NO₃ + 6H₂O + 8C — NH₃ + 9OH^– ……………………..(2)

Now multiplying equation (1) by 4 and then adding to equation (2), we get,

4Zn + 16OH- + NO, + 6H₂O→ 4ZnO₂ + NH₃ + 90H- + 8H₂O

Or, 4Zn + 7OH^–+ NO^–₃→ 4ZnO₂^– + NH₃ + 2H₂O

It is the balanced equation of the reaction in ionic form. Expressing the above equation in molecular form

4Zn + 7NaOH + NaNO₃→ 4Na₂ZnO₂ + NH₃ + 2H₂O

It is the molecular form of the balanced equation of the reaction.

6. In the presence of HNO₃, sodium bismuthatic (NaHO₃) reacts with Mn(NO₃)₂ to produce coloured sodium permanganate (NaMnO₄) and itself gets reduced to bismuth nitrate.

Reaction: NaBIO₃ + Mn(NO₃) + UNO₂ →NaMnO₄ + Bi(NO₃) + H₂O The equation can be expressed in ionic form as— BIO₂ + Mn²⁺ → Bl³⁺ + MnO₄ + H₂O

Oxidation half-reaction: Mn²⁺ + 4H₂O → MnO₄^–+8H⁺→+5e ……………………(1)

Reduction half-reaction: BiO₃ + 6H⁺ + 2e — Bi³⁺ + 3H₂O…………………….(2)

Multiplying equation (1) by 2 and equation (2) by 5 and then adding them we get—

2Mn²⁺ + 8H₂O + 5BiO₃ ^– +30H⁺→ 2MnO₄^– + 16H⁺ + 5Bi³⁺ +15H₂O

2Mn²⁺ + 5BiO₃ + 14H⁺→ 5Bi³⁺+ + 2MnO₄^–  +7HO

This is the balanced ionic equation of the reaction. The equation in the molecular form stands as—

2Mn(NO₃)₂ + 5NaBiO₃+ 14HNO₃ →  5Bi(NO₃)₃ + 2NaMnO₄ + 7H₂O

Ionic reaction: IO₃^– + I^–+ H⁺→ I₂ + H₂O

Oxidation half-reaction: 2I^– → I₂ + 2e ……………………….(1)

Reduction half-reaction: 2 IO₃^– + 12H⁺+ 10 e → I₂ + 6H₂O ……………………….(2)

Multiplying equation (1) by 5 and then adding to equation (2) we get,

10I^– + 2IO₃^–+ 12H⁺ → 6I₂+ 6H₂O or, 5I^– + 1O₃^–+ 6H⁺ — 3I₂ + 3H₂O

This is the balanced ionic equation of the reaction.

Oxidation number method

In any redox reaction, the increase in the oxidation number of some of the atoms is balanced by the decrease in the oxidation number of some other atoms.

The steps which are to be followed while balancing the oxidation-reduction equation by this method are given below— After identifying the oxidant and reductant, the skeleton equation for the reaction is written.

• The elements of the reactants and the products changing oxidation number are identified and the oxidation number of the concerned atoms is mentioned.
• The reactant in which the element undergoes a decrease in oxidation number is the oxidant, while the reactant in which the element undergoes an increase in oxidation number is the reductant.
• As oxidation and reduction are complementary to each other, die increase and decrease in oxidation numbers should necessarily be equal, For this reason, the respective formulae of the oxidants and reductants are multiplied by a possible suitable integer so that the changes in oxidation numbers arc equalised.
• For balancing the equation, it may sometimes be necessary to multiply the formula of other substances participating in the reaction by a suitable integer.
• If the reactions are carried out in an acidic medium, then, to balance the number of O -atoms, one molecule of O^–is added for each O -atom to the side of the equation deficient in oxygen.

To balance the number of -atoms, H+ ions are added to the side deficient in hydrogen.

In case of a reaction occurring in an alkaline medium, to balance the number of O -atoms on both sides of the equations, for each O -atom one molecule of water is added to the side deficient in O -atoms and to the opposite side two OH- ions for each water molecule are added.

Again for balancing the number of FI^– atoms on both sides of the equation, for each 2 -atom one OH^– ion is added to the side which contains excess 2 -atoms and the same number of FI₂O molecules are added to the other side.

Example

1. Copper dissolves in concentrated HNO₃ to form Cu(NO₃)₂, NO₂ and H₂O

Reaction:

In the given reaction, the increase in oxidation number of Cu -atom =(+2)-0 = 2 unit (oxidation) and the decrease in oxidation number of N -atom =(+5)-(+4) = 1 unit (reduction).

To nullify the effect of increase and decrease in the oxidation numbers, the ratio of the number of Cu -atoms and Cu(NO₃)₂  molecules in the reaction should be 1:2. So the equation may be written as

Cu + 2HNO₃ → Cu(NO₃)₂ + 2NO₂ + H₂O

Now, to produce one molecule of Cu(NO₃)₂ two NO₂ radicals i.e. two molecules of UNO₂ are required. Hence in the reaction further addition of two molecules of HNO₃ is necessary. So the balanced equation is expressed as

Cu + 4HNO₃→ Cu(NO₃)₂ + 2NO₂ + 2H₂O

Now, to produce one molecule of Cu(NO₃)₂, two NO₃ radicals i.e. two molecules of UNO₂ are required.

Hence in the reaction further addition of two molecules of HNO₂ is necessary. So the balanced equation is expressed as

Cu+4HNO₃ Cu(NO₃)^{→ 2+}2NO²⁺2H₂O

When H₂S gas is passed through chlorine water H₂SO₄ is produced.

Reaction:

In this reaction, an increase in the oxidation number of S = (+6) — (— 2) = 2 units (oxidation) and a decrease In the oxidation number of Cl = 0 – (— 1 ) I unit (reduction). So decrease In oxidation number for two (‘,1 -atoms or I molecule of Cl₂ -2 unit.

To neutralise the effect of Increase and decrease In oxidation number in the given equation, the number of molecules of H₂S and Cl₂ should be in the ratio of 2: i.e., 1: <1.

Therefore, the equation becomes

H₂S+4CI₂+HCl+H₂SO₄

Balancing the number of 11 and O -atoms on both sides gives the balanced equation —

3. NH₃ gas when passed over heated Cut) produces Cu, N₂ and H₂O.

In this reaction, increase In oxidation number of N=0-(-3) = 3 unit (oxidation) and decrease In oxidation number of Cu =(+2)-0 = 2 unit (reduction). As, in a redox reaction, the total increase in oxidation number is equal to the total decrease In oxidation number, the number of molecules of CuO and NH₃ in the reaction should be in the ratio of 3:2. Hence, the balanced equation will be—

3CuO+2NH₃→3Cu+N₂+3H₂O

4. In the reaction between KMnO₄ and H₂O₂, the products obtained were K₂SO₂ MnSO₂, H₂O And O₂.

Reaction:

In this reaction increases in oxdination number of O = 0-(-1)=1 (oxidaxtion) and dexrease in oxidation number of MN= (+7)-(+20)

= 5 unit (reduction).

The total increase in the oxidation number of two 0 -atoms presents one molecule of H₂O₂

To balance the decrease and increase in oxidation numbers, the ratio of the number of KMnO₂ and H₂O, molecules in the equation for the reaction will be 2:5.

Again from 2 molecules of KMnO₄ and 5 molecules of H₂O₂, 2 molecules of MnSO₂ and 5 molecules of O₂ are produced respectively. Thus the equation becomes—

2KMnO₄ + 5H₂O₂+ H₂SO₄→ K₂SO₄+ 2MnSO₄ + 5O₂ + H₂O

Again, for the formation of 1 molecule of K₂SO₄ and 2 molecules of MnSO₄, three SO₄– radicals are required and hence three H₂SO₄ molecules are necessary on the left-hand side. Besides this, the total number of H-atoms in 5 molecules of H₂O₂ and 3 molecules of H₂SO₄ = 16.

These H-atoms produce water molecules. Therefore, 8 molecules of H₂O are to be placed on the right-hand side. So the balanced equation will be—

2KMnO₄ + 5H₂O₂ + 3H₂SO₄ → K₂SO₄ + 2MnSO₄ + 5O₂+ 8H₂O

5. White phosphorus and concentrated NaOH react together to yield NaH₂PO₂ and PH₃. Reaction

The increase in oxidation number of P [P to NaH₂PO₂ ] = +1- 0 = 1 unit (oxidation). The decrease in oxidation number of P [P to PH₃] = 0-(-3) = 3 unit (reduction). To balance the increase and decrease in oxidation number, three P atoms for oxidation and one P -atom for reduction are required. Thus four P -atoms are necessary.

Now, in the oxidation of P, NaH₂PO₂ and its reduction, PH₃ are formed. So the oxidation of three P atoms forms 3 molecules of NaH₂PO₉ and for this, three NaOH molecules are required. Again 1 atom of P reduction produces 1 molecule of PH₃. So the equation will be

P₄+3NaOH + H₂O→ 3NaH₂PO₂ + PH₃

On the right side of the equation, there are 6 oxygen atoms, out of which 3 atoms will come from 3 molecules of NaOH and for the rest three atoms, 3 molecules of H₂O will be necessary. Hence, the balanced equation will be

P₄+ 3NaOH + H₂O → 3NaH₂PO₂ + PH₃

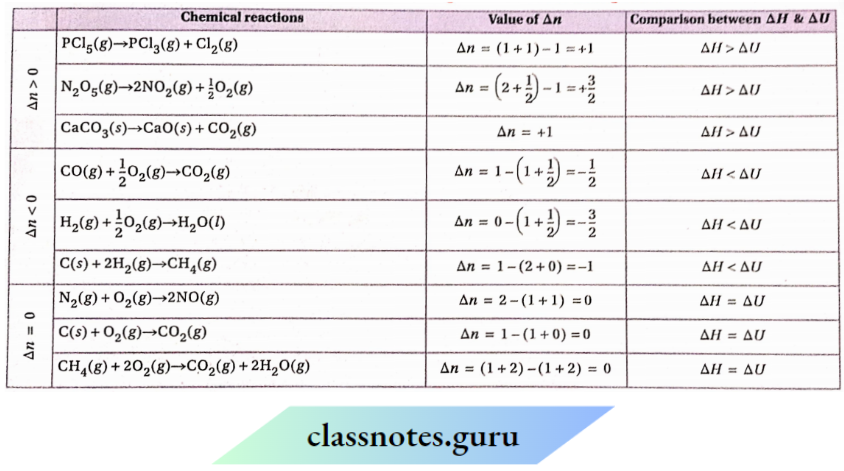
6. In NaOH solution, Zn reacts with NaNO₃ to yield Na₂ZnO₂, NH₃ and H₂O.

Reaction:

In the reaction, an increase in the oxidation number of Zn =(+2) -0 = 2 unit (oxidation) and a decrease in the oxidation number of N =(+5)-(-3) = 8 unit (reduction). As the increase and decrease in oxidation number in the reaction must be equal, the number of Zn -atoms and the number of molecules of NaNO₃ should be in the ratio of 4:1. Now, 1 molecule of NaNO₃ and 4 atoms of Zn produce 1 molecule of NH3 and 4 molecules of Na₂ZnO₂ respectively. Therefore the reaction is—

4Zn + NaNO₃ + NaOH →4Na₂ZnO₂ + NH₃ + H₂O

Again formation of 4 molecules of Na₂ZnO₂ requires 8 Na -atoms, out of which 1 atom is supplied by 1 molecule of NaNO₃. Additional 7 Na -atoms come from NaOH on the left side. To balance H -atoms on both sides, 1 H₂O molecule is to be placed on the right side. Thus the balanced equation will be —

4Zn + NaNO₃ + 7NaOH →4Na₂ZnO₂ + NH₃ + 2H₂O

7. In the reaction between Cr₂O₃ and Na₂O₂, Na₂CrO₄ and NaOH are produced.

Reaction:

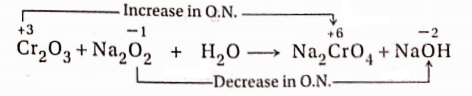
In this reaction, an increase in the oxidation number of Cr = (+6)- (+3) = 3 unit (oxidation) and a decrease in the oxidation number of O =(- 1 )-(- 2) = 1 unit (reduction). Thus a total increase in the oxidation number of two Cr -atoms = 3 × 2 = 6 units and the total decrease in the oxidation number of two O -atoms = 1× 2

= 2 units.

To balance the increase and decrease in oxidation number, the ratio of Cr₂O₃ and Na₂O₂ should be =1:3. Now 2 molecules of Na₂CrO₄ are produced from 1 molecule of Cr₂O₃. Hence the equation will be as follows—

Cr₂O₃+3Na₂O₂+H₂O→ 2Na₂CrO₄+NaOH

If Na, H and O- atoms are balanced on both sides, the balanced equation will stand as

Cr₂O3+ 3Na₂O₂ + H₂O→ 2Na₂CrO₄ + 2NaOH

8. White phosphorus reacts with copper sulphate solution to produce Cu, H₃PO₄ and H₂SO₄.

Reaction:

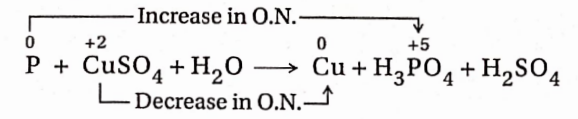
In this reaction, an increase in the oxidation number of P = (+5)-0 = 5 unit (oxidation) and a decrease in the oxidation number of Cu =(+2)-0 = 2 unit (reduction).

Since the increase and decrease in oxidation number must be equal, in the given reaction, the ratio of the number of atoms of P and the number of CuSO₄ molecules should be in the ratio of 2: 5. Again 2 molecules of H₃PO₄ and five Cu -atoms will be produced respectively from two P atoms and five CuSO₄ molecules. As a result, the equation becomes—

2P + 5CuSO₄ + H₂O→ 5Cu + 2H₃PO₄ + H₂SO₄

To balance the number of SO²‾₄ radicals on both sides of the equation, 5 molecules of H₂SO₄ are to be added to the right-hand side ofthe equation.

2P + 5CuSO₄ + H₂O→5Cu + 2H₃PO₄ + 5H₂SO₄

Now, the total number of H-atoms present in 2 molecules of H₃PO₄ and 5 molecules of H₂SO₄ =16. So, for balancing the number of H-atoms, 8 water molecules are to be placed on the left-hand side. So, the balanced equation will be

2P + 5CuSO₄ + 8H₂O→5Cu + 2H₃PO₄ + 5H₂SO₄

9. Aluminium powder when boiled with caustic soda solution yields sodium aluminate and hydrogen gas.

Reaction:

Aluminium is oxidised in this reaction to produce sodium aluminate. On the other hand, the H -atoms of NaOH and H₂O are reduced to produce H₂. Therefore, the change in oxidation number in the reaction may be shown as follows—

The increase in oxidation number of A1 = (+3) -0 = 3 unit (oxidation), the decrease in oxidation number of 1 H atom of NaOH molecule \(=(+1)-\left(\frac{1}{2} \times 0\right)\) (reduction) and decrease in oxidation number of 2 H -atoms
of water molecule = 2 x (+1) -2×0 = 2 unit(reduction).

Hence, the total decrease in oxidation number for the Hatoms in 1 molecule of NaOH and 1 molecule of H₂O =3 unit.

Since, in a chemical reaction, the increase and decrease in oxidation number are the same, the ratio of the number of A1 atoms, NaOH molecule and water molecules in the given reaction should be =1: 1: 1.

⇒ \(\mathrm{Al}+\mathrm{NaOH}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{NaAlO}_2+\frac{1}{2} \mathrm{H}_2+\mathrm{H}_2\)

Hence, the given reaction may be represented as:

Now, to express the number of molecules of reactants and products in terms of whole numbers, both sides of the equation should be multiplied by 2.

So, the balanced equation will be as follows:

⇒ \(\mathrm{Al}+\mathrm{NaOH}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{NaAlO}_2+\frac{1}{2} \mathrm{H}_2+\mathrm{H}_2\)

Determination of equivalent mass of an element or compound in disproportionation reaction:

If in oxidation and reduction reaction, the change in oxidation number of any element or an element of any compound participating in a disproportionation reaction be n1 and n2 respectively and M be the molecular mass of that element or compound, then the equivalent mass of that element or compound \(=\frac{M}{n_1}+\frac{M}{n_2}\)

In oxidation reaction (P4— change in oxidation number of each P -atom = 1 unit. So the total change in oxidation number of four P-atoms = 4 × 1 =4 units.

In the reduction reaction, (P₄→PH₃), the change in oxidation number of each P-atom is 3 units. So the total change in oxidation number of four P-atoms = 4×3 = 12 units.

Thus in this reaction, the equivalent mass of P₄.

⇒ \(\frac{M}{4}+\frac{M}{12}=\frac{4 \times 31}{4}+\frac{4 \times 31}{12}=31+10.33 \text {= } 41.33\)

∴ The atomic mass of p = 31

Redox Titration

A process by which a standard solution of an oxidant (or a standard solution of a reductant) is completely reacted with a solution of an unknown concentration of a reductant (or with a solution of an unknown concentration of an oxidant) in the presence of a suitable indicator is called redox titration.

In a redox titration, an oxidant (or a reductant) reacts completely with an equivalent amount of a reductant (or an oxidant). Therefore, in a redox titration, the number of grams equivalent of oxidant = number of grams equivalent of reductant.

Types of redox titrations

1. Permanganometry titration

A titration in which KMnO₄ solution is used as the standard solution. In this titration, no indicators are needed.

Example:

The amount of iron present in an acidic ferrous ion (Fe²⁺) solution can be estimated by titrating the solution with a standard solution of KMnO₄.

Reaction:

MnO₄ + 5Fe²⁺ + 8H+ → Mn²⁺ + 5Fe3+ + 4H₂O …………………….(1)

Oxidation reaction: Fe²⁺→ Fe3+ + e

Reduction reaction: MnO₄ ^–+ 8H⁺ + 5e → Mn²⁺ + 4H₂O

So, in this reaction, the equivalent mass of Fe²⁺ — an atomic mass of Fe and the equivalent mass of KMnO₄ \(=\frac{1}{5} \times\) Molecular or formula mass of KMnO₄

According to the reaction (1), 1 mol of KMnO₄ = 5 mol of Fe²⁺ ions or, 1000 mLof 1 mol of KMnO₄ solution = 5 × 55.85g of Fe²⁺ ions or, 1 mLof l(M) KMnO₄ solution = 0.2792g of Fe²⁺ ions mL of 5(N) KMnO₄ solution = 0.2792g of Fe²⁺ ions. [In the given reaction, the normality of KMnO₄ solution is five times its molarity.]

lmL of (N) KMnO₄ solution = 0.05585g of Fe²⁺ ions

2.  Dichromatometry titration

A ptration in which a standard solution of potassium dichromate (K₂Cr₂O₇) is used.

In this titration, sodium or barium diphenylamine sulphonate or diphenylamine is used as an indicator.

Example:

The amount of iron present in an acidic ferrous ion (Fe²⁺) solution can be calculated by titrating the solution with a standard solution of K₂Cr₂O₇.

Reaction: 

Cr₂O₇+ 14H+ + 6Fe²⁺→ 2Cr³⁺+ 6Fe²⁺ + H₂O …………….(1)

In reaction (1), the equivalent mass of Fe²⁺ is equal to the atomic mass of Fe, & the equivalent mass of K₂Cr₂O₇ is equal to one-sixth of its molecular or formula mass.

According to the reaction (1), 1 mol of K₂Cr₂O₇ H 6mol of Fe²⁺ ions

Or, 1000mL of 1M K₂Cr₂O₇ = 6 × 55.85 g of Fe²⁺ ions

Or, lmLof1M K₂Cr₂O₇ solution s 0.3351g of Fe²⁺ ions

Or, lmL of 6N K₂Cr₂O₇ solution s 0.3351g of Fe²⁺ ions

[In the given reaction, the normality of K₂Cr₂O₇ solution is six times its molarity.]

lmL of IN K₂Cr₂O₇ solution = 0.05585g of Fe²⁺ ions

3. Iodometry titration

In this titration, KI in excess is added to a neutral or an acidic solution of an oxidant. Consequently, the oxidant quantitatively oxidises I^– ions (reductant), to form I₂. The liberated I₂ is then titrated with a standard Na₂S₂O₃ solution using starch as an indicator.

The amount of liberated iodine is calculated from the volume of standard Na₂S₂O₃ solution consumed in one titration. After the amount of liberated iodine is known, one can calculate the amount of oxidant by using the balanced chemical equation for the reaction of oxidant with iodine.

Example:

Iodometric titration is often used for quantitative estimation of Cu²⁺ ions. The addition of excess KI to a neutral or an acidic solution of Cu²⁺ ions results in oxidation of 1 to I2 and reduction of Cu²⁺ to Cu⁺.

So, in the reaction(l), the equivalent mass of \(\mathrm{Cu}^{2+}=\frac{2 \times \text { atomic mass of } \mathrm{Cu}}{2}=\text { atomic mass of } \mathrm{Cu}\)

The reaction of I₂ with Na₂S₂O₃ is:

⇒  \(2 \mathrm{~S}_2 \mathrm{O}_3^{2-}+\mathrm{I}_2 \rightarrow \mathrm{S}_4 \mathrm{O}_6^{2-}+2 \mathrm{I}^{-}\)

In this reaction, Oxidation reaction:

⇒  \(2 \mathrm{~S}_2 \mathrm{O}_3^{2-} \rightarrow \mathrm{S}_4 \mathrm{O}_6^{2-}+2 e\)

Reduction reaction: I₂ + 2e → 2I^–

Therefore, the equivalent mass of Na₂S₂O₃

⇒ \(\frac{2 \times \text { molecular or formula mass of } \mathrm{Na}_2 \mathrm{~S}_2 \mathrm{O}_3}{2}\)

= molecular or formula mass of Na₂S₂O₃

Equivalent mass of I₂ \(=\frac{\text { molecular mass of } \mathrm{I}_2}{2}=\text { atomic mass of } \mathrm{I}\)

According to the reactions (1) and (2), 2mol of Cu²⁺ = 1 mol of I2 and 2 mol of Na₂S₂O₃ s 1 mol of I₂

Therefore, 2mol of Na₂S₂O₃= 2 mol of Cu²⁺ or, 1 mol of Na₂S₂O₃ = l mol of Cu²⁺ = 63.5g of Cu²⁺ or, l mol of lM Na₂S₂O₃ solution = 63.5 g of Cu²⁺ or, 1 mol of IN Na₂S₂O₃ solution = 63.5gof Cu²⁺ [As in the reaction of Na₂S₂O₃ with I₂, the equivalent mass of Na₂S₂O₃ is equal to its molecular mass].

Question 1. The reaction Fe₂O₃(s) + 3CO(gH→2Fe(s) + 3CO₂(g) is carried out separately in a closed vessel and an open vessel. In which case do you expect a higher yield of CO₂(g)?
Answer:

If the reaction Fe₂O₃(s) + 3CO(g)→2Fe(s) + 3CO₂(g) is carried out in a closed vessel, an equilibrium is established between the reactants and the products. As a result, the reaction vessel always contains a mixture of reactants and products.

On the other hand, if the reaction is carried out in an open vessel, CO2(g) formed in the reaction diffuses out from the vessel and mixes with the air and does not have the opportunity to react with Fe(s).

As a result, the reaction becomes irreversible and goes to completion. At the end of the reaction, the vessel only contains Fe(s). Since the reaction reaches completion in an open vessel, the yield of CO₂(g) will be higher in this condition.

Question 2. If a reversible reaction is carried out in a closed vessel, the reactant(s) is/are never used up completely. Explain the reaction with an example.
Answer:

When a reversible reaction is carried out in a closed vessel, an equilibrium is established between the reactants and the products.

As a result, the reaction system always contains a mixture of reactants and products. In other words, a reversible reaction occurring in a closed vessel never gets completed. Consequently, the reactants are never used up.

Question 3. 2BrP₂(g) ⇌ Br₂(g) + 5F₂(g); At constant temperature, how the increase in pressure will affect the following at equilibrium— Equilibrium constant, Position of the equilibrium, and yield of the product?
Answer:

Pressure does not affect the magnitude of the equilibrium constant.

The given reversible reaction involves a decrease in several gas molecules in the backward direction. So, increasing pressure at the equilibrium of the reaction will favor the backward reaction Consequently, the yield of the product will decrease.

Question 4. Write the conjugate bases of the following acids and give the reason: HN₃, CH₃OH, [Al(H₂O)₆]³⁺, NH₄⁺, HPO₄^2-, H₂O₂, OH^–
Answer:

According to the Bronsted-Lowry concept, an acid is a substance that can donate protons. The species formed when an acid donates a proton is called the conjugate base of the acid. The conjugate base of an acid has one fewer H-atom than the acid.

Therefore, the conjugate bases of HN₃, CH₃OH, [Al(H₂O)₆]³⁺, NH₄⁺, HPO₄^2-, H₂O₂ and OH^– are N^–₃, CH₃O^–, [Al(H₂O)₅OH]²⁺, NH₃, PO^3-₄, HO^–₂ and O^-2, respectively.

Question 5. Write the conjugate acids of the following bases and give the reason: OH^–, H₂PO^–₄, O^2-, HS^–, SO^2-₃, H₂O, HCO₃^–, NH^–₂, NH₃, H^–, C₆H₅NH₂, S₂O₈^2- CO₃^2-
Answer

According to the Bronsted-Lowry concept, a base is a proton acceptor. When a base accepts a proton, the conjugate acid of the die base is formed. The conjugate acid of a base contains one more H-atom than the base.

Therefore, the conjugate acids of OH^–, H₂PO₄ , O^2-, HS^–, SO^2–₃, H₂O, HCO^–₃, NH^–₂ , NH₃, H^–, C₆H₅NH₂ , S₂O₈^2- and CO₃^2-– are H₂O , H₃PO₄ , OH^– , H₂S, HSO^–₃, H₃O⁺, H₂CO₃, NH₃, NH₄⁺+, H₂, C₆H₅NH⁺₃, HS₂O₈^– and HCO^–₃ respectively.

Question 6. To find out the equilibrium constant (K) of a reaction, it is compulsory to mention the balanced equation of the reaction—why?
Answer:

The value of the equilibrium constant (K) depends on how the balanced equation of the reaction is written, example the formation of H₂ (g) from H₂ (g) and I₂ (g) can be written in two different ways

⇒ \(\mathrm{H}_2(g)+\mathrm{I}_2(g) \rightleftharpoons 2 \mathrm{HI}(g) \text { (2) } \frac{1}{2} \mathrm{H}_2(g)+\frac{1}{2} \mathrm{I}_2(g) \rightleftharpoons \mathrm{HI}(g)\)

Both 1 and 2 express the same reaction but the coefficients of reactants and products are different. As a result, the value of the equilibrium constant (K) for the reaction will not be the same in the above two cases.

Question 7. Find Out K_p/K_c for the solutions \(\mathrm{CO}(g)+\frac{1}{2} \mathrm{O}_2(g) \rightleftharpoons \mathrm{CO}_2(g)\)
Answer:

We know that \(K_p=K_c(R T)^{\Delta n}.\)

For the given reaction \(\Delta n=1-\left(1+\frac{1}{2}\right)=-\frac{1}{2}\)

Thus \(K_p=K_c(R T)^{-\frac{1}{2}}\)

⇒ \(\frac{K_p}{K_c}=\frac{1}{\sqrt{R T}}\)

Question 8. By what factor will the concentration of H₃O⁺ ions in an aqueous solution be increased or decreased if its pH is increased by one unit?
Answer:

If the pH of an aqueous solution be x, then [H₃O⁺] in the solution = 10^-pH

= 10-x mol.L^-1

Increasing the pH of this solution by one unit makes

pH =  1 + x.So, (H₃O⁺) In the solution

= 10^-pH = 10^-(1+x)

= \(\frac{10^{-x}}{10} \mathrm{~mol} \cdot \mathrm{L}^{-1}\)

Question 9. Why is the ionic product of water at 50 greater than that at 25°C?
Answer:

Ionisation of water \(\left[2 \mathrm{H}_2 \mathrm{O}(l) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q)\right]\)

Is an endothermic process. The equilibrium constant referring to the ionization equilibrium of water is called the ionic product of water (K_w). As the process is endothermic, Kw increases with the temperature rise. Thus, Kw of water at 50 °C is greater than that at 25 °C.

Question 10. The pH of solution A is twice that of solution B. If the concentrations of H₃O⁺ ions in A and B are x (M) and y (M), respectively, then what is the relation between x and y?
Answer:

Given:

pH of the solution A = 2 × pH of the solution B,

⇒ \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_A=x \mathrm{~mol} \cdot \mathrm{L}^{-1} \text { and }\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_B=y \mathrm{~mol} \cdot \mathrm{L}^{-1} \text {. }\)

∴ \(-\log _{10}\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_A=2 \times-\log _{10}\left[\mathrm{H}_3 \mathrm{O}^{+}\right]_B\)

Or, \(x=y^2 \text { or, } y=\sqrt{x}\)