CBSE Solutions For Class 10 Mathematics Chapter 14 Statistics

Class 10 Maths Statistics

Question 1. Find the mean by the direct method:

Solution:

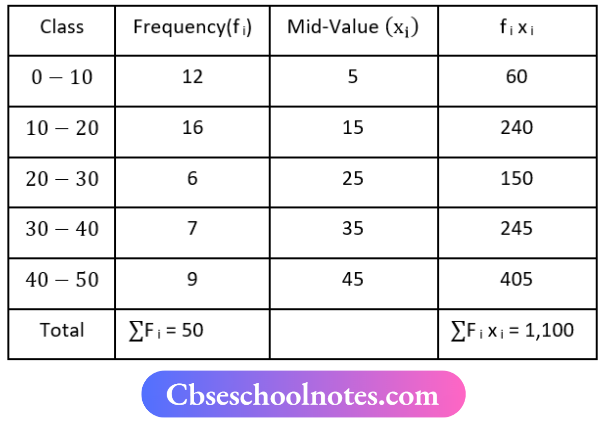
Now,

mean \(\bar{x}=\frac{\sum f_{i x_i}}{\sum f_i}=\frac{1100}{50}=22\)

Question 2. Find the mean using the Direct Method:

Read and Learn More Class 10 Maths

Solution:

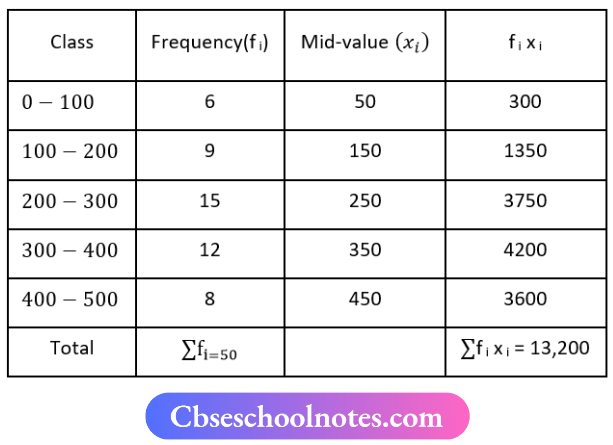
Now, mean \(\bar{x}=\frac{\sum f_{i x i}}{\sum f_i}=\frac{13,200}{50}=264\)

Question 3. The mean of the following frequency distribution is 25. Find the value of P using the direct method:

Solution:

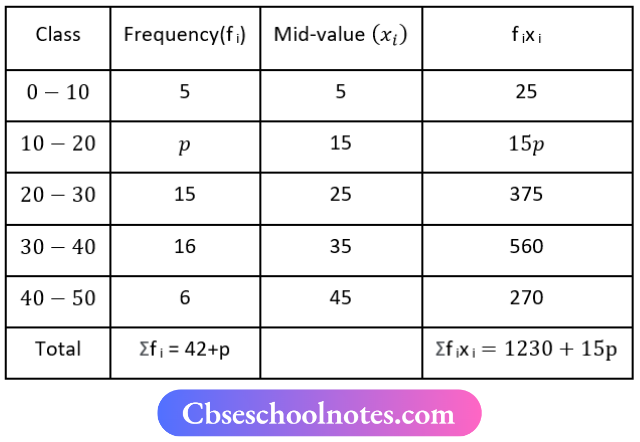
Now, Mean

⇒ \(\bar{x}=\frac{\sum f_{i x i}}{\sum f_i}\)

⇒ \(\bar{x}=\frac{1230+15 p}{42+p}\)

⇒ \(25=\frac{1230+15 P}{42+P}\)

⇒ 1050 + 25P = 1230 + 15P

⇒ 25P – 15P = 1230 + 15P

⇒ 10P = 180

⇒ P = \(\frac{180}{10}\)

P = 18

Question 4. The mean of the following distribution is 54. Find the value of P using the direct method:

Solution:

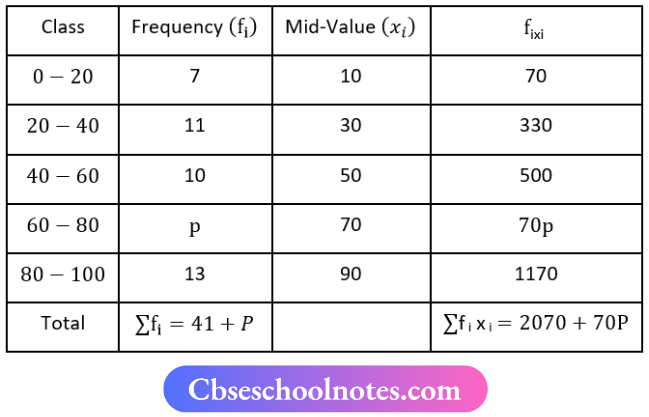
Now, Mean \(\bar{x}=54\)

⇒ \(\bar{x}=\frac{\sum f_{i x_i}}{\sum f_i}\)

54 = \(\frac{2070+70 p}{41+P}\)

2214+54p=2070+70P

70P-54P = 2214-2070

16P = 144

P = \(\frac{144}{16}\)

P = 9

Question 5. Find the mean from the following table using the Short Cut Method:

Solution:

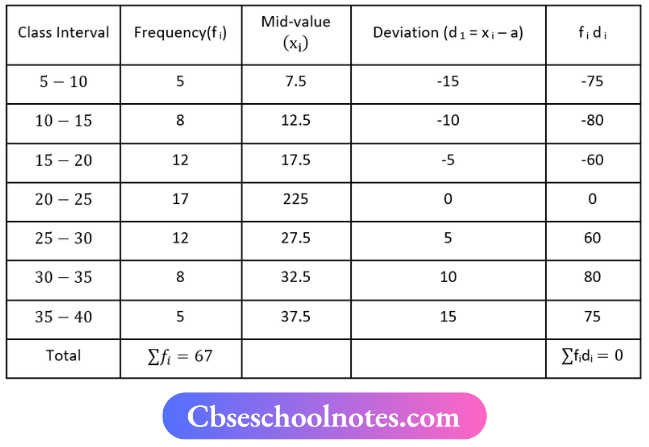
Now, Mean a = 22.5

Mean \(\bar{x}=a+\frac{\sum f_{i d i}}{\sum f_i}\)

⇒ \(\bar{x}=22.5+\frac{0}{67}\)

⇒ \(\bar{x}=22.5\)

Question 6. Find the mean from the following table using the step. deviation method:

Solution:

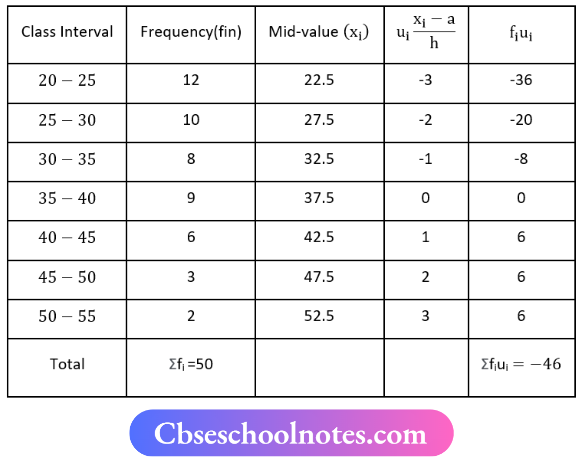
Now, a = 37.5, h = 5

Mean \(\bar{x}=a+\frac{\sum f_{i u_i}}{\sum f_i} \times h\)

⇒ \(\bar{x}=37.5+\frac{-46}{50} \times 5\)

⇒ \(\bar{x}=37.5-\frac{46}{10}\)

⇒ \(\bar{x}=\frac{375-46}{10}\)

⇒ \(\bar{x}=\frac{329}{10}\)

⇒ \(\bar{x}=32.9\)

Question 7. Find the mean from the following table using the step deviation method:

Solution:

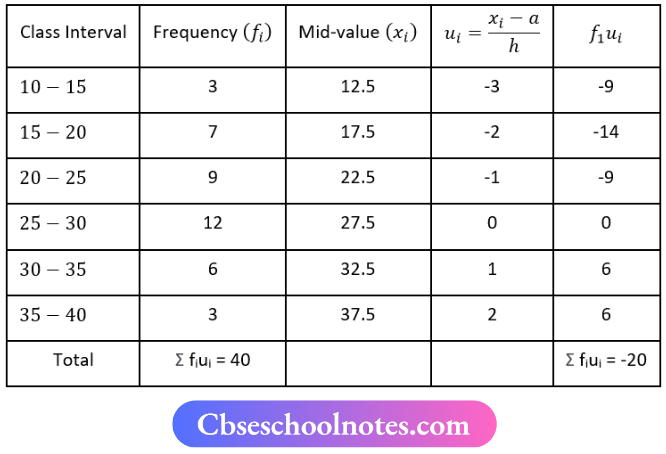
Now, a = 27.5, h = 5

mean \(\bar{x}=a+\frac{\sum f_i u_i}{\sum f_i} \times h\)

⇒ \(\bar{x}=27.5+\frac{-20}{40} \times 5\)

⇒ \(\bar{x}=\frac{220-20}{8}\)

⇒ \(\bar{x}=\frac{200}{8}\)

⇒ \(\bar{x}=25\)

Question 8. Find the median from the following data:

Solution:

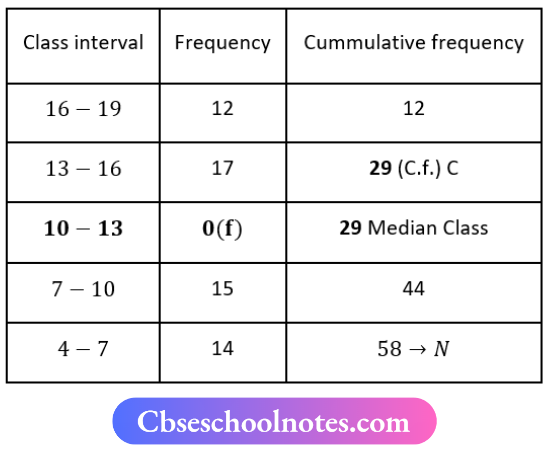
Here, N = 58

∴ For Median class \(\frac{N}{2}=\frac{58}{2}=29\)

∴ Median class = 10-13

Here l₁ = 10, l₂ = 13

⇒ i = 13-10 = 3

f = 0, C.f = 29

∴ Median M = \(l_1+\frac{\left(\frac{N}{2}-c\right)}{f} \times i\)

M = \(10+\frac{29-29}{0} \times 3\)

M = \(10+\frac{0}{0} \times 3\)

M = 10

Question 9. Find the Median from the following data:

Solution:

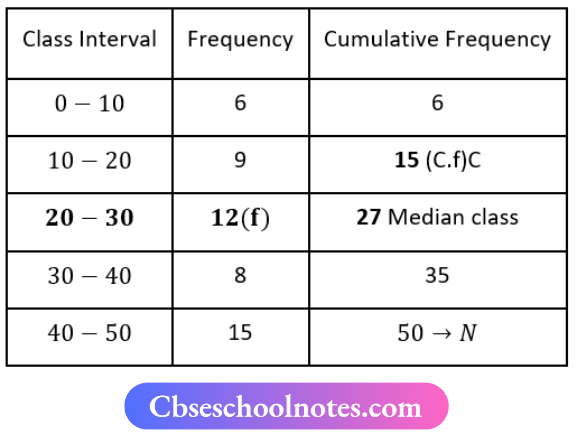
Here, N = 50

⇒ \(\frac{N}{2}=\frac{50}{2}=25\)

=25

∴ Median Class = 20-30

Now, l₁ = 20, l₂ = 30

i = 30-20 = 10

f = 12, C = 15

and Median M = \(l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i\)

M = \(20+\frac{(25-15)}{12} \times 10\)

M = \(20+\frac{10}{6} \times 5\)

M = \(\frac{120+50}{6}\)

M = \(\frac{170}{6}\)

M = 28.33

Question 10. Find the median from the following data:

Solution:

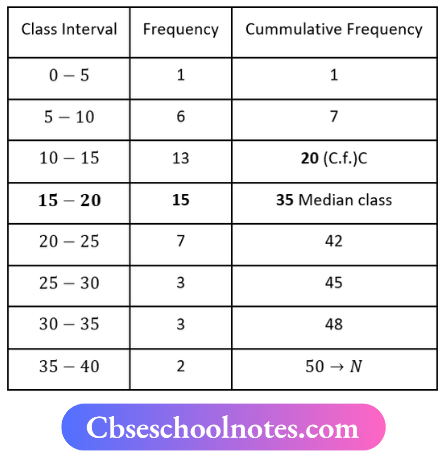
Here N = 50

⇒ \(\frac{N}{2}=\frac{50}{2}=25\)

∴ The median class is 15-20

Now, l₁ = 15, l₂ = 20, i = 20-15 = 5, f = 15, C = 20

and Median M = \(l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i\)

M = \(15+\frac{25-20}{15} \times 5\)

M = \(\frac{45+5}{3}\)

M = \(\frac{50}{3}\)

M = 16.67

Question 11. Find the Median for the following frequency distribution:

Solution:

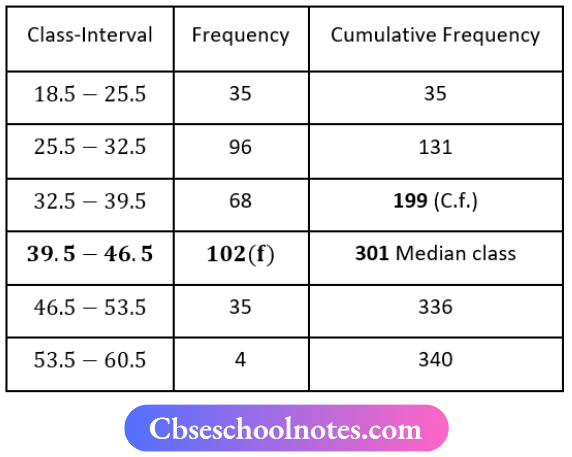
Now, N=340

⇒ \(\frac{N}{2}=\frac{340}{2}=170\)

∴ Median class = 39.5-46.5

∴ l₁ = 39.5, l₂ = 46.5, i= 46.5-39.5 = 7, f = 102, C = 199

Median M = \(l_1+\frac{\left(\frac{N}{2}-c\right)}{f} \times i\)

M = \(39.5+\frac{(170-199)}{102} \times 7\)

M = \(39.5-\frac{29}{102} \times 7\)

M = \(39.5-\frac{203}{102}\)

M = \(\frac{4029-203}{102}\)

M = \(\frac{3826}{102}\)

M = 36.5

Question 12. Find the Median for the following frequency distribution:

Solution:

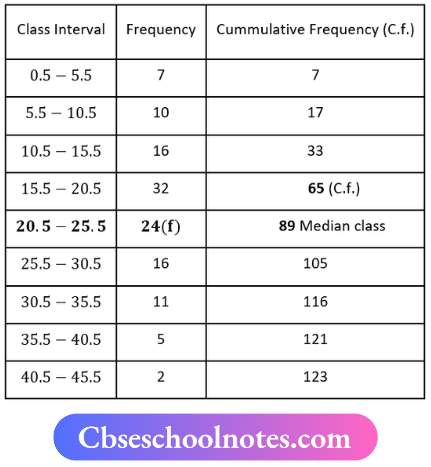
Here N = 123

⇒ \(\frac{N}{2}=\frac{123}{2}=61.5\)

∴ Median Class = 20,5-25.5

l₁ = 20.5, l₂ = 25.5, i = 25.5-20.5 = 5, f = 24, C = 65

Median M = \(l_1+\frac{\left(\frac{N}{2}-C\right)}{F} \times i\)

M = \(20.5+\frac{(61.5-65)}{24} \times 5\)

M = \(20.5-\frac{3.5}{24} \times 5\)

M = \(\frac{492-17.5}{24}\)

M = \(\frac{474.5}{24}\)

M = 20.1

Question 13. If the Median of the following frequency distribution is 32.5. Find the value of F.

Solution:

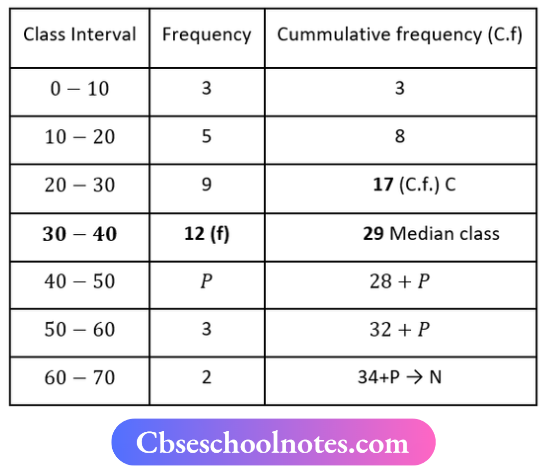
Here N = 34+ P

⇒ \(\frac{N}{2}=\frac{34+P}{2}\)

Median = 325 ⇒ Median class=30-40

∴ 1₁ = 30, l₂ =40, i = 40-30=10

f = 12, C = 17

M = \(l_1+\frac{\left(\frac{N}{2}-c\right)}{f} \times i\)

32.5 = \(30+\frac{\left(\frac{34+p}{2}-17\right)}{12} \times 10\)

32.5-30 = \(\frac{10}{12}\left(\frac{34+P}{2}-17\right)\)

2.5 = \(\frac{5}{6}\left(\frac{34+p-34}{2}\right)\)

2.5 = \(\frac{5 P}{12}\)

30 = 5P

P = \(\frac{30}{5}\)

P = 6

Question 14. Determine the median for the following income distribution:

Solution:

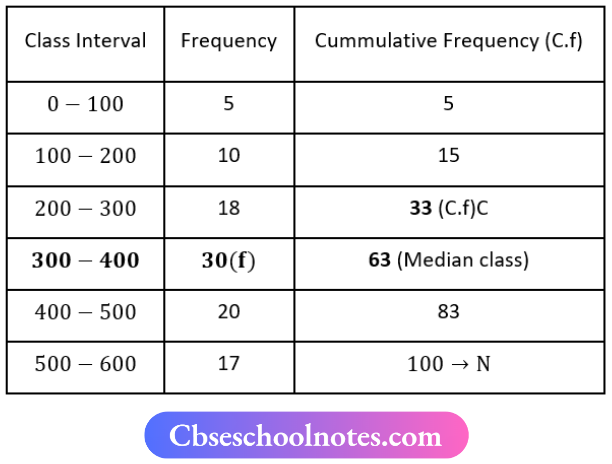
Here N = 100

⇒ \(\frac{N}{2}=\frac{100}{2}=50\)

∴ Medion class = 300-400

∴ l₁ = 300, l₂ = 400, i= 400-300 = 100, f = 30, C = 33

M = \(l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i\)

M = \(300+\frac{50-33}{30} \times 100\)

M = \(300+\frac{17}{30} \times 100\)

M = \(\frac{9000+1700}{30}\)

M = \(\frac{10700}{30}\)

M = 356.67

Question 15. Find the mode of the following frequency distribution:

Solution:

Clearly, the modal class is 60-80 as it has the maximum frequency

∴ l = 60, f₁ = 12, f₀ = 10, f₂ = 6, h = 20

Mode M = \(l+\frac{f_1-f_0}{2 f_1-f_0-f_2} \times h\)

M = \(60+\frac{12-10}{2(12)-10-6} \times 20\)

M = \(60+\frac{2}{24-16} \times 20\)

M = \(60+\frac{2}{8} \times 20\)

M = \(\frac{480+40}{8}\)

M = \(\frac{520}{8}\)

M = 65

Question 16. Given below is the frequency distribution of the heights of players in a school;

Solution:

Clearly, the modal class is 165.5-1685 as it has a maximum frequency

∴ l = 165.5, f₁ = 142, f₀ =118, f₂ = 127, h=3

Mode = \(l+\frac{f_1-f_0}{2 f_1-f_0-f_2} \times h\)

M = \(165.5+\frac{142-118}{2(142)-118-127} \times 3\)

M = \(165.5+\frac{24}{284-245} \times 3\)

M = \(165.5+\frac{24}{39} \times 3\)

M = \(\frac{6454.5+72}{39}\)

M = \(\frac{6526.5}{39}\)

M = 167.35

Question 17. Find the mode of the following frequency distribution:

Solution:

Clearly, the modal class is 50-60, as it has the maximum frequency

∴ l = 50, f₁ = 11, f₀ = 9, f₂ = 6, h = 10

Mode = \(\ell+\frac{f_1-f_0}{2 f_1-f_0-f_2} \times h\)

M = \(50+\frac{11-9}{2(11)-9-6} \times 10\)

M = \(50+\frac{2}{22-15} \times 10\)

M = \(50+\frac{2}{7} \times 10\)

M = \(\frac{350+20}{7}\)

M = \(\frac{370}{7}\)

M = 52.86

Question 18. The following distribution represents the height of 160 students in a class;

Solution:

Clearly, the modal class is 155-160 as it has the maximum

∴ l = 155, f₁ = 38, f₀ =30, f₂ =24, h=5

Mode = \(l+\frac{f_1-f_0}{2 f_1-f_0-f_2} \times h\)

M = \(155+\frac{38-30}{2(38)-30-24} \times 5\)

M = \(155+\frac{8}{76-54} \times 5\)

M = \(155+\frac{40}{22}\)

M = \(\frac{3410+40}{22}\)

M = \(\frac{3450}{22}\)

M = 156.82

Question 19. The following table gives the weekly wage of workers in a factory:

Find (1) the mean (2) the modal class (3) the mode

Solution:

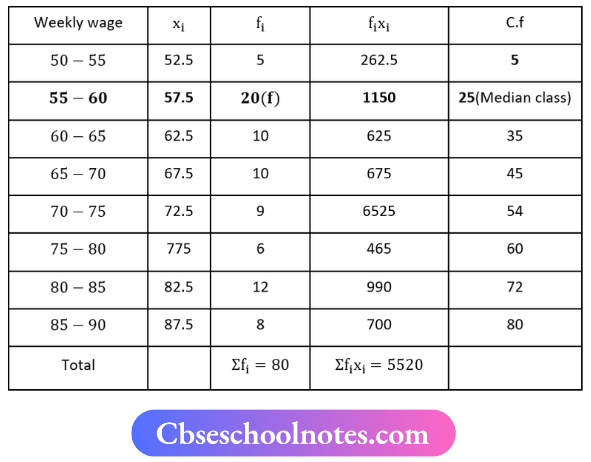
1. Mean:

Mean = \(\frac{\sum f_{i x i}}{\sum f_i}=\frac{5520}{80}\)

= 69

2. Modal class = 55-60

3. Mode: clearly, the Modal class is 55-60 it has the maximum frequency

l = 55, f₁ = 20, f₀ = 5, f₂ = 10, h = 5

M = \(l+\frac{f_1-f_0}{2 f_1-f_0-f_2} \times h\)

M = \(55+\frac{20-5}{2(20)-5-10} \times 5\)

M = \(55+\frac{15}{40-15} \times 5\)

M = \(55+\frac{15}{25} \times 5\)

M = \(\frac{1375+75}{25}\)

M = \(\frac{1450}{25}\)

M = 58

Question 20. The mode of the following Series is 36. Find the missing frequency in it:

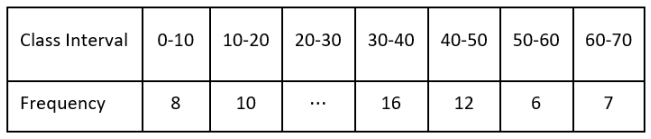
Solution:

Clearly, 30-40 is the modal class as mode 36 lies in this class

Here l = 30, f₁ = 16, f₀ = x (Say), f₂ = 12 and h = 10 and mode 36

Mode (M) = \(\ell+\frac{f_1-f_0}{2 f_1-f_0-f_2} \times h\)

36 = \(30+\frac{16-x}{2(16)-x-12} \times 10\)

36 = \(30+\frac{16-x}{32-x-12} \times 10\)

36 = \(30+\frac{16-x}{20-x} \times 10\)

36 – 30 = \(\frac{16-x}{20-x} \times 10\)

6(20-x) = 10(16-x)

120-6x = 160-10x

10x-6x = 160-120

4x = 40

x = \(\frac{40}{4}\)

x = 10

Question 21. Compute the mode of the following data:

Solution:

Clearly, Modal class 29.5 – 29.5 as it has the maximum frequency

∴ l = 19.5, f₁ = 23, f₀ = 16, f₂ = 15, h = 10

M = \(\ell+\frac{f_1-f_0}{2 f_1-f_0-f_2} \times h\)

M = \(19.5+\frac{23-16}{2(23)-16-15} \times 10\)

M = \(19.5+\frac{7}{46-31} \times 10\)

M = \(\frac{292.5+70}{15}\)

M = 24.17

Question 22. Find the mean, Median, and mode of the following data:

Solution:

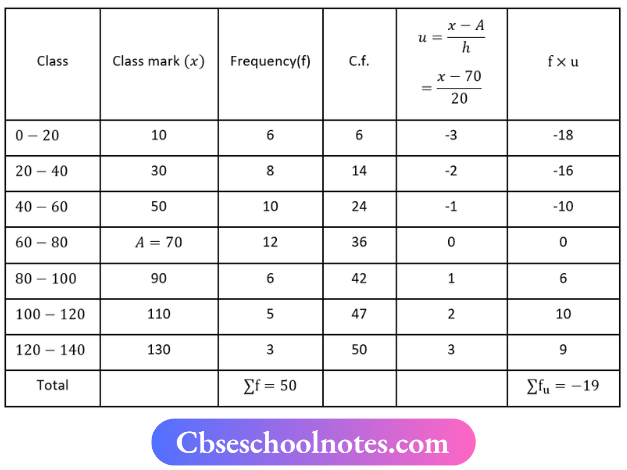
let assumed mean A = 70, h = 20, Ef = 50, and Σfu = -19

Mean \(\bar{x}=A+\left[h \times \frac{\sum f_u}{\sum f}\right]\)

⇒ \(\bar{x}=70+\left[20 \times \frac{-19}{50}\right]\)

⇒ \(\bar{x}=70+[20 x-0.38]\)

⇒ \(\bar{x}=70-7.6\)

⇒ \(\bar{x}=62.4\)

Here N = 50

⇒ \(\frac{N}{2}=\frac{50}{2}\) = 25

Cumulative frequency just greater than 25 is 36 and the Corresponding class is 60-80.

∴ l₁ = 60, f = 12, l₂ = 80, C = 24, i = 80-60 = 20

Now, median (M) = \(l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i\)

M = \(60+\frac{(25-24)}{12} \times 20\)

M = \(60+\frac{1}{12} \times 20\)

M = \(\frac{720+20}{12}\)

M = \(\frac{740}{12}\)

M = 61.66

Mode = 3(Median)-2(Mean)

Mode = 3(61.66)-2(62.4)

= 184.98-124.8

M = 60.18

Question 23. 100 Surnames were randomly picked from a local directory and the distribution of a number of letters of the English alphabet in the Surname was obtained as follows:

Solution:

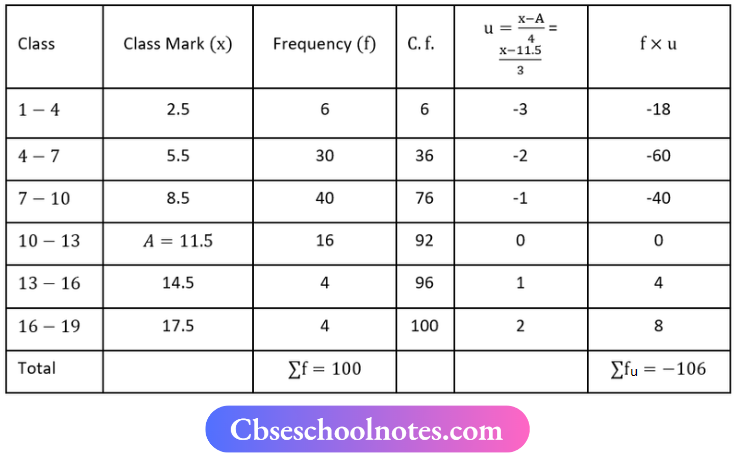
let assumed mean A = 11.5, h = 3, Σf = 100, Σfu = -106

Mean \(\bar{x}=A+\left[h \times \frac{\sum(f u)}{\sum f}\right]\)

⇒ \(\bar{x}=11.5+\left[3 \times \frac{-106}{100}\right]\)

⇒ \(\bar{x}=11.5+[3 \times-1.06]\)

⇒ \(\bar{x}=11.5-3.18\)

⇒ \(\bar{x}=8.32\)

Here, N = 100

⇒ \(\frac{N}{2}=\frac{100}{2}\)

= 50

Cumulative frequency just greater than 50 is 76 and the corresponding class is 10-13

∴ l₁ = 7, f = 40, l₂ = 10, C = 36, i = 10-7 = 3

Median (M) = \(\ell+\frac{\left(\frac{N}{2}-C\right)}{f} \times i\)

M = \(7+\frac{50-36}{40} \times 3\)

M = \(7+\frac{14}{40} \times 3\)

M = \(\frac{280+42}{40}\)

M = \(\frac{322}{40}\)

M = 8.05

Mode = 3(Median)-2(Mean)

= 3(8.05)-2(8-32)

= 24.15-16.64

M = 7.51

Question 24. The following table gives the daily income of such workers of a factory:

Find the mean, mode, and median of the above data.

Solution:

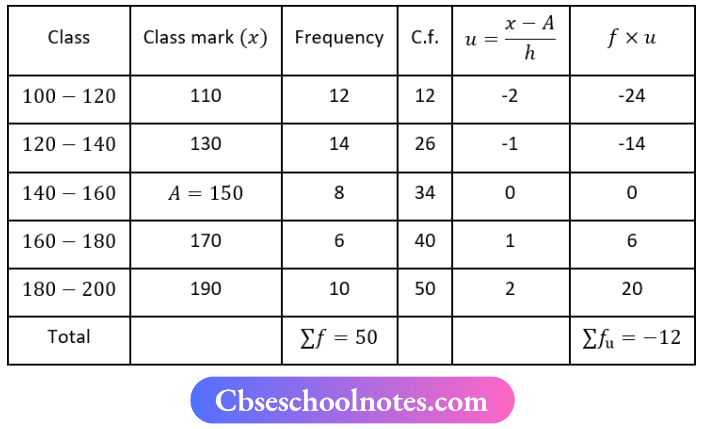
let assumed mean A = 150, h = 20, Σf = 50, Σfu = -12

Mean \(\bar{x}=A+\left[h \times \frac{\sum f_4}{\sum P}\right]\)

⇒ \(\bar{x}=150+\left[20 \times \frac{-12}{50}\right]\)

⇒ \(\bar{x}=150+[20 x-0.24]\)

⇒ \(\bar{x}=150-4.8\)

⇒ \(\bar{x}=145.2\)

Here N = 50

⇒ \(\frac{N}{2}=\frac{50}{2}=25\)

Cumulative frequency just greater than 25 is 36 and the Corresponding is 120-140

∴ l₁ = 120, f = 14, l₂ = 140, C = 12, i = 140-120 = 20

Now, Median = \(l_1+\frac{\left(\frac{N}{2}- C\right)}{f} \times i\)

⇒ \(120+\frac{(25-12)}{14} \times 20\)

⇒ \(120+\frac{13}{14} \times 20\)

⇒ \(\frac{1680+260}{14}\)

⇒ \(\frac{1940}{14}\)

M = 138.57

Mode = 3(Median) – 2 (Mean)

M = 3(138.57)-2((45.2)

= 415.71-290.4

= 125.31

Question 25. A Survey regarding the heights (in cm) of so girls in a class was conducted and the following data was obtained:

Solution:

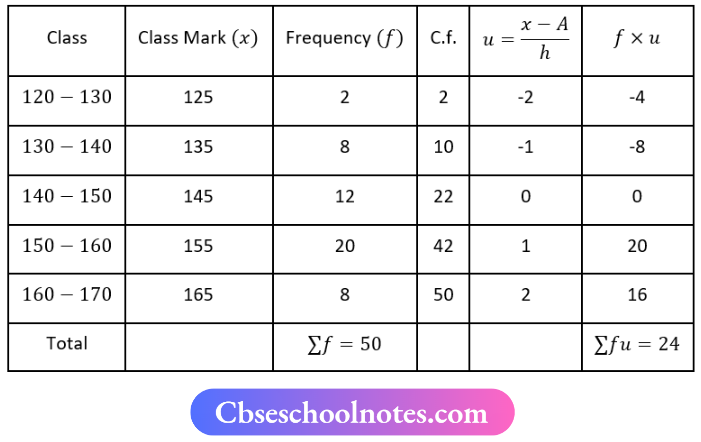
Let assumed Mean A=145, h=10, Σf=50, and Σfu=24

Mean \(\bar{x}=A+\left[h \times \frac{\sum f_u}{\sum f}\right]\)

⇒ \(\bar{x}=145+\left[10 \times \frac{24}{50}\right]\)

⇒ \(\bar{x}=145+[10 \times 0.48]\)

⇒ \(\bar{x}=145+4.8\)

⇒ \(\bar{x}=149.8 \mathrm{~cm}\)

Here N = 50

⇒ \(\frac{N}{2}=\frac{50}{2}=25\)

Cumulative frequency just greater than 25 is 42 and the Corresponding is 150-160

l₁ = 150, f = 20, l₂ = 160, C = 22, i = 160-150 = 10

Now, Median (M) = \(l_1+\frac{\left(\frac{N}{2}-c\right)}{F} \times i\)

⇒ \(150+\frac{(25-22)}{20} \times 10\)

⇒ \(150+\frac{30}{20}\)

⇒ \(\frac{3000+30}{20}\)

⇒ \(\frac{3030}{20}\)

= 151.5 cm

Mode = 3(Median)-2(Mean)

Mode = 3(151.5)-2(149.8)

= 454.5-299.6

= 154.9

Question 26. The table below shows the daily expenditure on food of 30 households in a locality:

Solution:

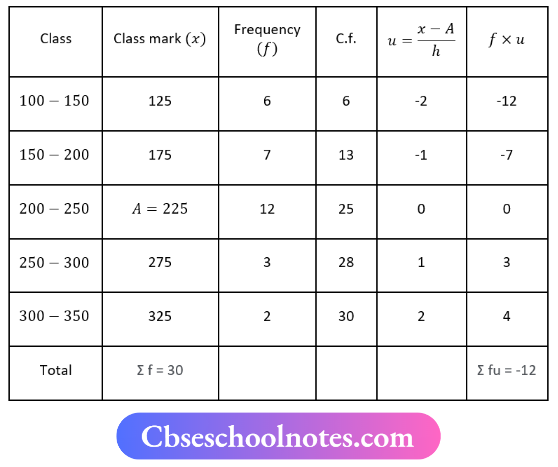
Let assumed mean A=225, h = 50, Σf=30, Σfu = -12

Mean \(\bar{x}=A+\left[h \times \frac{\sum f u}{\sum f}\right]\)

⇒ \(\bar{x}=225+\left[50 \times \frac{-12}{30}\right]\)

⇒ \(\bar{x}=225+[50 \times -0.4]\)

⇒ \(\bar{x}=225-20\)

⇒ \(\bar{x}=205\)

Here, N = 30

⇒ \(\frac{N}{2}=\frac{30}{2}=15\)

Median Class = 200-250

l₁ = 200, f = 12, l₂ = 250, C = 13, i = 250-200 = 50.

Median (M) = \(l_1+\frac{\left(\frac{N}{2}-c\right)}{F} \times i\)

M = \(200+\frac{15-13}{12} \times 50\)

M = \(\frac{2400+100}{12}\)

M = \(\frac{2500}{12}\)

M = 208.33