Kristensmith Taylor

CBSE Class 12 Physics Chapter 11  Dual Nature Of Radiation And Matter Multiple Choice Questions And Answers

Question 1. The speed acquired by a free electron when accelerated from rest through a potential difference of 100V is:

1. 6 x 10⁶ m s^-1
2. 3 x 10⁶ m s^-1
3. 4 x 10⁵ m s^-1
4. 2 x 10³ m s^-1

Answer: 1. 6 x 10⁶ m s^-1

Read and Learn More Important Questions for Class 12 Physics with Answers

Question 2. Photons of energy 1 eV and 2.5 eV successively illuminate a metal whose work function is ________.

1. 1:2
2. 2:1
3. 3:1
4. 1:3

Answer: 1. 1:2

K.E_max for 1 photon = 1-0.5 = 0.5eV

K.E_max for 2 photon = 2.5-0.5 = 2eV

⇒ \(\frac{K E_1}{K E_2}=\frac{0.5}{2}=\frac{1}{4} \quad\left(K=\frac{1}{2} m v^2\right)\)

So speed \(\left(\frac{v_1}{v_2}=\frac{1}{2}\right)\)

Question 3. The de-Broglie wavelength associated with a particle with rest mass m₀ and moving with the speed of light in vacuum is ________.

1. \(\frac{\mathrm{h}}{\mathrm{m}_0 \mathrm{c}}\)
2. 0
3. ∞
4. \(\frac{\mathrm{m}_0 \mathrm{c}}{\mathrm{h}}\)

Answer: 2. 0

Question 4. Photoelectric effect represents __________

1. Electron has a wave nature
2. Light has a particle nature
3. Light has a wave nature
4. None of these

Answer: 2. Light has a particle nature

Question 5. If the momentum of an electron is required to be the same as that of a wave having 5200 Å wavelength, its velocity should be ______ ms^-1

1. 10³
2. 1.4 x 10³
3. 1.39 x 10³
4. 2.8 x 10³

Answer: 3. 1.39 x 10³

⇒ \(\lambda=\frac{h}{m v}\)

∴ \(v=\frac{h}{m \lambda}=\frac{6.62 \times 10^{-34}}{9.1 \times 10^{-31} \times 5200 \times 10^{-10}}=1.39 \times 10^3 \mathrm{~m} / \mathrm{s}\)

Question 6. To increase the de Broglie wavelength of an electron from 0.5 x 10^-10 m to 10^-10 m, its energy should be _________.

1. Increased to four times
2. Halved
3. Doubled
4. Decreased to the fourth part

Answer: 4. Decreased to fourth part

⇒ \(\lambda=\frac{\mathrm{h}}{\sqrt{2 \mathrm{mK}}}\) ⇒ \(\lambda \propto \frac{1}{\sqrt{\mathrm{K}}}\)

∴ \(K \propto \frac{1}{\lambda^2}\)

λ → twice, K must be \(\left(\frac{1}{4}\right)^{th}\)

Question 7. The energy of the photon is E = hf and its momentum is \(P=\frac{h}{\lambda}\), where λ, is the wavelength of the photon with this assumption speed of the light wave is

1. \(\frac{P}{E}\)
2. \(\frac{E}{P}\)
3. EP
4. \(\left(\frac{E}{P}\right)^2\)

Answer: 2. \(\frac{E}{P}\)

⇒ \(E=h f=\frac{h c}{\lambda}\)

⇒ \(c=\frac{E \lambda}{h} \quad\left(\frac{\lambda}{h}=\frac{1}{P}\right)\)

∴ \(c=\frac{E}{P}\)

Question 8. Which of the following physical quantities has the dimension of Planck constant (h)?

1. Angular momentum
2. Force
3. Energy
4. Power

Answer: 1. Angular momentum

Question 9. If the photoelectric effect is not seen with the ultraviolet radiations in a given metal, photoelectrons may be emitted with the _________.

1. Radio waves
2. Infrared waves
3. X-rays
4. Visible light

Answer: 3. X-rays

Question 10. The work function of _______ is the lowest.

1. Platinum
2. Caesium
3. nickel
4. Copper

Answer: 2. Caesium

Question 11. The value of slopping potential depends on ________ of incident light.

1. Intensity
2. Frequency
3. Momentum
4. Velocity

Answer: 2. Frequency

Question 12. Monochromatic light of frequency 6 x 10¹⁴ Hz is produced by laser. Each photon has an energy = ________ J.

1. 6 x 10¹⁴
2. 4 x 10^-19
3. 4 x 10^-20
4. 6 x 10^-14

Answer: 2. 4 x 10^-19

E = hv

E = 6.62 x 10^-34 x 6 x 10¹⁴ = 39.72 x 10^-20 = 3.972 x 10^-19 = 4 x 10^-19 J

Question 13. For a given frequency of incident radiation, slopping potential ________.

1. Does not depend on the intensity
2. Is inversely proportional to the intensity
3. Is directly proportional to the intensity
4. Is inversely proportional to the square of intensity.

Answer: 1. Does do not depend on the intensity

Question 14. The slope of a graph of stopping potential versus frequency of incident radiation is _________.

1. c
2. h
3. \(\frac{h}{e}\)
4. \(\frac{e}{h}\)

(where h = Planck’s constant and e = charge of an electron)

Answer: 3. \(\frac{h}{e}\)

Question 15. De-Broglie wavelength of a bullet of mass 0.040 kg travelling at the speed of 1 km/s is _________ m.

1. 1.7 x 10^-35
2. 4.04 x 10^-24
3. 1. 1 x 10^-32
4. 3 x 10^-32

Answer: 1. 1.7 x 10^-35

∴ \(\lambda=\frac{h}{m v}=\frac{6.62 \times 10^{34}}{0.040 \times 1000}=1.655 \times 10^{-35}=1.7 \times 10^{-35} \mathrm{~m}\)

CBSE Class 12 Physics Chapter 11  Dual Nature Of Radiation And Matter Assertion And Reason

For question numbers 1 to 6 two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (1), and (2). (3) and (4) as given below.

1. Both A and R are true and R is the correct explanation of A
2. Both A and R are true but R is NOT the correct explanation of A
3. A is true but R is false
4. A is false and R is also false

Question 1. Assertion: The photoelectric effect demonstrates the wave nature of light.

Reason: The number of photoelectrons is proportional to the frequency of light

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 2. Assertion: At saturation, the photoelectric current is maximum.

Reason: At saturation, all the electrons emitted from the cathode can reach the anode.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 3. Assertion: A photon is not a material particle. It is a quantum of energy.

Reason: The photoelectric effect demonstrates the wave nature of radiation.

Answer: 3. A is true but R is false

Question 4. Assertion: Photo electric current increases if the distance between the cathode and anode is increased.

Reason: The momentum of a photon is directly proportional to its wavelength.

Answer: 4. A is false and R is also false

Question 5. Assertion: The photosensitivity of a metal is high if its work function is small.

Reason: Work function = hv₀, where v₀ is the threshold frequency.

Answer: 2. Both A and R are true but R is NOT the correct explanation of A

Question 6. Assertion: In his study of photoelectric emission, Hallwachs connected a negatively charged zinc plate to an electroscope. He found that negatively charged particles were emitted from the zinc plate under the action of visible light.

Reason: An uncharged zinc plate becomes positively charged when it is irradiated by visible light.

Answer: 4. A is false and R is also false

CBSE Class 12 Physics Chapter 11  Dual Nature Of Radiation And Matter Short Questions And Answers

Question 1. A proton and a particle are accelerated through the same potential difference. Which one of the two has

1. Greater de-Broglie wavelength, and
2. Less kinetic energy? Justify your answer

Answer:

∴ \(\lambda=\frac{h}{p}=\frac{h}{\sqrt{2 q V m}}\)

1. α – particle: \(\frac{h}{\sqrt{2 q_{\alpha} V_{m_{\alpha}}}}=\lambda_\alpha\) ( ∵ \(\begin{aligned} & \mathrm{q}_\alpha=2 \mathrm{q}_{\mathrm{p}}  & \mathrm{m}_{\mathrm{\alpha}}=4 \mathrm{~m}_{\mathrm{p}} \end{aligned}\))

proton: \(\frac{h}{\sqrt{2 q_p V m_p}}=\lambda_p\)

Clearly, \(\lambda_{\mathrm{p}}>\lambda_\alpha \text { as } \mathrm{m}_\alpha>\mathrm{m}_{\mathrm{p}} \ and \mathrm{q}_\alpha>\mathrm{q}_{\mathrm{p}}\)

So, a proton has a greater de-broglie wavelength.

2. As \(\frac{1}{2} m v^2=q_V ;(\text { K.E. })_{\mathrm{p}}<(\text { K.E. })_{\alpha} \text { as } \mathrm{q}_{\mathrm{p}}<\mathrm{q}_{\alpha}\)

So, a proton has less K.E

Question 2.

1. Draw graphs showing the variation of photoelectric current with applied voltage for two incident radiations of equal frequency and different intensities. Mark the graph for the radiation of higher intensity.
2. Name the phenomenon which shows the quantum nature of electromagnetic radiation.

Answer:

The graph I₂ corresponds to radiation of higher intensity

2. Photoelectric effect (PEE)

Question 3. Plot a graph showing the variation of de-Broglie versus \(\frac{1}{\sqrt{V}}\) where V is accelerating the potential for two particles A and B carrying the same charge but of masses m₁, m₂, (m₁ > m₂). Which one of the two represents a particle of smaller mass and why?

Answer:

As, \({\lambda} =\frac{h}{\sqrt{2 \mathrm{mqV}}}\)

Graph: Slope of verses \(\frac{1}{\sqrt{V}}\) graph will be inversely prop, to the square root of the mass of the particles. Now, the slope of B is greater and it shows that its mass is smaller.

Question 4. The wavelength λ of a photon and the de-Broglie wavelength of an electron have the same value. Show that the energy of a photon is (2λmc/h) limes the kinetic energy of electron: where m. c and h have their usual meaning.

Answer:

⇒ \(E_{\text {photon }}=\frac{h c}{\lambda}\) → (1) \(\lambda_{\text {photon }}=\lambda_{\text {electron }}={\lambda}\)

⇒ \(E_{\text {elcetron }}=\frac{h^2}{2 m \lambda^2}\) → (2) ( ∵ \(\lambda=\frac{\mathrm{h}}{\sqrt{2 \mathrm{mE}_{\text {electron }}}}\)))

Dividind (1) by (2), \(\frac{\mathrm{E}_{\text {photon }}}{\mathrm{E}_{\text {electron }}}=\frac{2 \mathrm{mc \lambda}}{\mathrm{h}}\)

Question 5. Calculate the dc-Broglic wavelength of the electron orbiting in the n = 2 stale of hydrogen atom.

Answer:

The velocity of an e^– in the first orbit (n = 1) of the hydrogen atom, v = 2.18 x 10⁶ m/s.

Now, the velocity of e^– in the second orbit (n = 2) of the hydrogen atom will be given as, v’ = v/n

∴ v’ = 1.09 x 10⁶ m/s

So mv’ = 9.9 x 10^-25

Putting the values in \(\lambda=\mathrm{h} / \mathrm{mv}^{\prime}=\frac{6.6 \times 10^{-34}}{9.9 \times 10^{-25}}=6.68 Å\)

Question 6.

1. Define the intensity of radiation based on a photon picture of light. Write its S.I. unit.
2. Draw a plot showing the variation of the de-Broglie wavelength of an electron as a function of its K.E.

Answer:

The intensity of radiation is defined as the energy associated with several photons incident/could from a unit surface area in unit time.

i.e. \(\text { Intensity }=\frac{\text { Energy }}{\text { Area } \times \operatorname{time}}\)

SI unit:

∴ \(\frac{\text { joule }}{m^2-s} \text { or } \mathrm{W}-\mathrm{m}^{-2}\)

∵ \(\lambda=\frac{\mathrm{h}}{\sqrt{2 \mathrm{mE}}}\)

Question 7.

1. Name the factor on which photoelectric emission from a surface depends.
2. Define the term ’threshold frequency’ for a photosensitive material.

Answer:

1. Metal should be photo-sensitive.
2. For a given photosensitive material, threshold frequency is the minimum frequency of radiation that is required for photoelectric emission from the material.

Question 8.

1. Plot a graph showing the variation of photocurrent v/s collector potential for three different intensities I₁ < I₂ < I₃, two of which (I₁ and I₂) have the same frequency v and the third has frequency v₁ > v₂.
2. Explain the nature of the curves based on Einstein’s equation.

Answer:

2. From. eV₀ = hv- hv₀ [Clearly stopping potential (V₀) depends on incident freq.(v)]

or \(V_0=\frac{h}{e} v-\frac{h}{e} v_0\)

So. for I₁ and I₂ intensities, freq. (v) is the same, hence for them stopping potential (V₀) is also equal.

Further, for. intensity having freq (v₁) stopping potential is more. (∵ V₁ > V₂ )

Question 9. For the light of wavelength 400 nm incident on the cathode of a photocell, the stopping potential is 6V. If the wavelength of incident light is increased to 600 nm. calculate the new stopping potential. (Take h =4.14 x 10^-15 eV. s)

Answer:

Given: \(\mathrm{hc}=4.14 \times 10^{-15} \times 3 \times 10^8 \mathrm{eV}s . \frac{\mathrm{m}}{\mathrm{s}}=12.42 \times 10^{-7} \mathrm{eVm}=12420 \mathrm{eVA}\)

λ₁= 400 nm, λ₂= 600 nm

V₀₁ =6V, V₀₂ = ?

∵ E = W₀ + K.E_max

K.E_max = E – W₀

⇒ \(\mathrm{eV}_0=\frac{h \mathrm{c}}{\lambda}-\mathrm{W}_0\) → (1)

So, \(\mathrm{eV}_{01}=\frac{h c}{\lambda_{1}}-W_0\) → (2)

⇒ \(\mathrm{eV}_{02}=\frac{\mathrm{hc}}{\lambda_2}-\mathrm{W}_0\) → (3)

Equation (3) – (2)

⇒ \(\left(\mathrm{V}_{02}-\mathrm{V}_{01}\right) \mathrm{e}=\mathrm{hc}\left(\frac{\mathrm{I}}{\lambda_2}-\frac{1}{\lambda_1}\right) \Rightarrow\left(\mathrm{V}_{02}-6\right)=\frac{\mathrm{hc}}{\mathrm{e}}\left(\frac{1}{600}-\frac{1}{400}\right)\)

∴ \(V_{02}-6=\frac{12420Å \mathrm{eV}}{\mathrm{e}}\left(-\frac{1}{12000}\right) \frac{1}Å; \quad V_{02}=\frac{-12420}{12000}+6=4.965 \mathrm{~V} \simeq 5 \mathrm{~V}\)

Question 10. Write three characteristic features in the photoelectric effect which cannot be explained based on the wave theory of light, but can be explained only using Einstein’s equation.

Answer:

1. The instantaneous ejection of photoelectrons.
2. Existence of threshold freq. for a metal surface.
3. The fact that the K.E. of the emitted electrons is independent of the intensity of the light depends on its frequency.

Question 11. Plot a graph showing the variation of photoelectric current with intensity of light. The work function for the following metals is given:

Na: 2.75 eV and Mo: 4.17 eV

Which of these will not give photoelectron emission from a radiation of wavelength 3300 Å from a laser beam? What happens if the source of the laser beam is brought closer?

Answer:

For, \(\lambda=3300Å . E=\frac{h c}{\lambda}=\frac{6.6 \times 10^{-34} \times 3 \times 10^8}{3300 \times 10^{-10}}=6 \times 10^{-19} \mathrm{~J}=\frac{6 \times 10^{-19}}{1.6 \times 10^{-19}} \mathrm{eV}=3.75 \mathrm{eV}\)

Incident energy 3.75 eV <4.17 eV, so the photoelectric effect will not take place in Mo (4. 17 eV). Photocurrent will increase in Na if the source of the laser beam is brought closer.

Question 11. State two important properties of photons which are used to write Einstein’s photoelectric equation. Define

1. Stopping potential and
2. Threshold frequency, using Einstein’s equation and drawing necessary plots between relevant quantities.

Answer:

1. The energy of a photon is proportional to the freq. of light. (E = hv)
2. Photons are quanta or discrete carriers of energy.

Stopping potential: In the experiment of the photoelectric effect, the value of the negative potential of the anode at which photoelectric current reduces to zero is called slopping potential for the given freq. of incident radiation.

Threshold freq.: For a given material, there exists a certain min. frequency below which no photoelectron can come out from the metal surface. This is called threshold frequency.

Question 12. Sketch the graphs showing the variation of stopping potential with the frequency of incident radiations for two photosensitive materials A and B having threshold frequencies v_A > v_B.

1. In which case is the slopping potential more and why?
2. Does the slope of the graph depend on the nature of the material used? Explain.

Answer:

From eV₀ = K_max = hv – Φ

eV₀ = hv- hv₀

∴ \(V_0=\frac{h v}{e}-\frac{h v_0}{e}\)

1. From the above equation, we can conclude, that the more threshold freq., the less would be the slopping potential (V₀). Here, v_0A > v_0B, hence slopping potential (V₀) is greater for B than A.

2. \(V_0=\left(\frac{h}{c}\right) v-\frac{h}{c} v_0(y=m x \pm c)\)

The slope of the above equation is \(\left(\frac{\mathrm{h}}{\mathrm{c}}\right)\) which is ‘independent’ of the nature of the material.

Question 13. Using a photon picture of light, show how Einstein’s photoelectric equation can be established. Write two features of the photoelectric effect which cannot be explained by wave theory.

Answer:

Einstein states that electromagnetic radiation energy is built up of discrete units called quanta of energy and has energy hv where ‘h’ is Planck’s constant and ‘V’ is the frequency of light.

In this phenomenon, an e^– absorbs a quantum of energy (hv), if the energy absorbed exceeds the minimum energy needed to escape from metal (Φ₀ ), e^– is emitted with maximum K.E.

∴ \(\mathrm{K}_{\text {max }}=h v-\phi_0\) [Einstein’s photo electric equation]

Two features of PEE which can’t be explained by wave theory

1. A min. frequency (threshold frequency) exists for diff. metals below which PEE is not possible.
2. PEE is an instantaneous phenomenon.

Question 14. Define the term ‘cut-off frequency” in photoelectric emission. The threshold frequency of a metal is f. When the light of frequency 2f is incident on the metal plate, the maximum velocity of photo-electrons is V₁. When the frequency of the incident radiation is increased to 5f, the maximum velocity of photo-electrons is v₂. Find the ratio: v₁: v₂.

Answer:

Cut-off Frequency: The minimum. frcq. of incident light which can emit photoelectrons from a material is known as cut-off frequency.

From eq. KE_max = hv- hv₀

⇒ \(\frac{1}{2} m v_1^2=h(2f)-hf=hf\) → (1)

⇒ \(\frac{1}{2} m v_2^2=h(5f)-hf=4 hf\) → (2)

∴ \(\frac{v_1^2}{v_2^2}=\frac{1}{4} \Rightarrow \frac{v_1}{v_2}=\frac{1}{2} \Rightarrow v_1: v_2=1: 2\)

Question 15. The given graph shows the variation of photo-electric current (I) with the applied voltage (V) for two different materials and for two different intensities of the incident radiation. Identify and explain using, Einstein’s photoelectric equation the pair of curves that correspond to

1. Different materials but the same intensity of incident radiation,
2. Different intensities but the same materials.

Answer:

1. (1,2) and (3,4) are diff. materials of the same intensity. The saturation current is the same but the stopping potential is different.
2. ( 1,3) and (2,4) have diff. intensities but the same materials. As saturation currents arc differently slopping potential is the same.

Question 16.

1. Calculate the frequency of a photon of energy 6.5 x 10^-19 J.
2. Can this photon cause the emission of an electron from the surface of Cs of work function 2.14 eV? If yes, what will be the maximum kinetic energy of the photoelectron?

Answer:

1. Energy E=hv

∴ \(v=\frac{E}{h}=\frac{6.5 \times 10^{-19}}{6.63 \times 10^{-34}}=0.98 \times 10^{15}=9.8 \times 10^{14} \mathrm{Hz}\)

2. Work function Φ₀ = 2.14 eV

The energy of photons in eV

∴ \(E=\frac{6.5 \times 10^{-19}}{1.6 \times 10^{19}}=4.06 \mathrm{eV}\)

KE_max = E – Φ₀ = 4.06 – 2.1 4 = 1 .92 eV

CBSE Class 12 Physics Chapter 11  Dual Nature Of Radiation And Matter Long Questions And Answers

Question 1. The photoelectric emission is possible only if the incident light is in the form of packets of energy, each having a definite value, more than the work function of the metal. This shows that light is not of wave nature but of particle nature. It is for this reason that photoelectric emission was accounted for by the quantum theory of light.

(1). Packets of energy are called

1. Electron
2. Quanta
3. Frequency
4. Neutron

Answer: 2. Quanta

(2). Energy associated with each photon

1. hc
2. mc
3. hv
4. hk

Answer: 3. hv

(3). Which of the following waves can produce the photoelectric effect

1. UV radiation
2. Infrared radiation
3. Radio waves
4. Microwaves

Answer: 1. UV radiation

(4). The work function of alkali metals is

1. Less than zero
2. Just equal to other metals
3. Greater than other metals
4. Quite less than other metals

Answer: 4. Quite less than other metals

Question 2. According to de-Broglie a moving material particle sometimes acts as a wave and sometimes as a particle or a wave is associated with a moving material particle which controls the particle in every respect. The wave associated with moving material particles is called matter wave or de-Broglie wave whose wavelength called dc-Broglic wavelength, is given by λ = h/mv.

(1). The dual nature of light is exhibited by

1. Diffraction and photoelectric effect
2. Photoelectric effect
3. Refraction and interference
4. Diffraction and reflection.

Answer: 1. Diffraction and photoelectric effect

(2). If the momentum of a particle is doubled, then its de-Broglie wavelength will:

1. Remain unchanged
2. Become four times
3. Become two times
4. Become half

Answer: 4. Become half

(3). If an electron and proton are propagating in the form of waves having the same X, it implies that they have the same:

1. Energy
2. Momentum
3. Velocity
4. Angular momentum

Answer: 2. Momentum

(4). Velocity of a body of mass m, having de-Broglie wavelength λ, is given by the relation:

1. v = λ h/m
2. v = λ m/h
3. v = λ/hm
4. v = h/λm

Answer: 4. v = h/λm

 CBSE Class 12 Physics Chapter 10 Wave Optics Multiple Choice Questions And Answers

Question 1. The distance between two slits in Young’s experiment is 0.2 mm. If the wavelength of the light used is 5000 Å, the angular position of the 5^th dark fringe from the central bright fringe is _________ rad.

1. 0.11
2. 1.1
3. 0.012
4. 0.0011

Answer: 3. 0.11

Read and Learn More Important Questions for Class 12 Physics with Answers

⇒ \(y_n=\frac{5 \lambda D}{d}\)

Angular position,

⇒ \(\theta_n=\frac{n \lambda}{d}\)

∴ \(\theta_5=\frac{5 \lambda}{d}=\frac{5 \times 5000 \times 10^{-10}}{0.2 \times 10^{-3}}\)

Question 2. The angular spread of the central maximum, in the diffraction pattern, does not depend on _________.

1. The Distance between the slit and the sources
2. Wavelength of light
3. Width of slit
4. Frequency of light

Answer: 1. The Distance between the slit and the sources

Question 3. In Young’s double-slit experiment, the width of the source slit is increased then _______.

1. The fringe pattern gets sharper and sharper
2. Instead of interference, diffraction appears
3. The angular distance between fringes increased
4. Fringe pattern gels less and less sharp

Answer: 4. Fringe pattern gels less and less sharp

Question 4. In a two-slit experiment, the screen is placed one meter away. When light of wavelength 500 nm is used the fringe separation is 0.5 mm. The distance between two slits is ________ mm.

1. 2
2. 5
3. 1
4. 4

Answer: 3. 1

⇒ \(\beta=\frac{\lambda \mathrm{D}}{\mathrm{d}}\)

⇒ \(\mathrm{d}=\frac{\lambda \mathrm{D}}{\beta}=\frac{500 \times 10^-9 \times 1}{0.5 \times 10^{-3}}\)

∴ d = 10^-3 m = 1nm

Question 5. If the phase difference between two waves is 6π radian, then the corresponding path difference is _________.

1. 6λ
2. λ
3. 2λ
4. 3λ

Answer: 4. 3λ

⇒ \(\frac{\Delta x}{\lambda}=\frac{\phi}{2 \pi}\)

⇒ \(\Delta x=\frac{6 \pi}{2 \pi} \times \lambda\)

∴ Δx = 3λ

Question 6. The intensity of a result wave obtained by the superposition of two waves is _______ amplitude of the resultant wave.

1. Directly proportional to the cube of
2. Directly proportional to
3. Directly proportional to the square of
4. Directly proportional to the square root of

Answer: 3. Directly proportional to the square of

 CBSE Class 12 Physics Chapter 10 Wave Optics Assertion And Reason

For question numbers 1 to 5, two statements are given: Assertion (A) and Reason (R). Select the correct answer to these questions from the codes (1), (2), (3) and (4) as given below.

1. Both A and R are true and R is the correct explanation of A
2. Both A and R are true but R is NOT the correct explanation of A
3. A is true but R is false
4. A is false and R is also false

Question 1. Assertion: If white light is used in YDSE, the central bright fringe will be white.

Reason: Because all the wavelengths produce their zero-order maxima at the same position.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 2. Assertion: Diffraction of sound waves is more easily observed than light waves.

Reason: Wavelength of sound waves is more as compared to light.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 3. Assertion: In interference light energy is redistributed.

Reason: There is no gain or loss of energy, which is consistent with the principle of energy conservation.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 4. Assertion: No interference pattern is detected when two coherent sources are infinitely close to each other.

Reason: The fringe width is inversely proportional to the distance between the two slits.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 5. Assertion: In Young’s experiment, the fringe width for dark fringes is different from that for white fringes.

Reason: In Young’s double slit experiment the fringes arc formed with a source of white light then only black and bright fringes are observed.

Answer: 4. A is false and R is also false

 CBSE Class 12 Physics Chapter 10 Wave Optics Short Questions And Answers

Question 1. Explain the formation of the fringes due to diffraction at a single slit, when the path difference of light waves from the ends of the slit on reaching a point on the screen is

1. λ
2. \(\frac{3 \lambda}{2}\)

Answer:

1. When the path difference is λ. then we get the first minima on screen.
2. When the Path difference is \(\frac{3 \lambda}{2}\) then we get the first secondary maxima on screen.

Question 2. How would the angular width of the central maximum of diffraction pattern be affected when

1. The width of the slit is decreased, and
2. Monochromatic light is replaced by polychromatic light. Justify your answers.

Answer:

In diffraction

⇒ \(\theta=\frac{2 \lambda}{d}\)

1. Angular width will increase \(\theta \propto \frac{1}{d}\)
2. The diffracted image gets dispersed into constituent colours of white light.

Question 3. Compare the interference pattern observed in Young’s double-slit experiment with the single-slit diffraction pattern, pointing out three distinguishing features.

Answer:

Question 4. Define the term wavefront. State Huygen’s principle. Consider a plane wave front incident on a thin convex lens. Draw a proper diagram to show how the incident wave from transverse through the lens and after refraction focuses on the focal point of the lens, giving the shape of the emergent wavefront.

Answer:

Wavefront: The Locus of all the points vibrating in the same phase is called wavefront.

Huygens Principle states that every point on a wavefront is a source of new disturbance which travels further in the form of secondary wavelets. These wavelets spread out in the forward direction at the same speed as the source wave. A new wavefront is a tangential surface to the secondary wavelets.

Question 5.

1. Derive Snell’s law on the basis of Huygens wave Ihcory when light is travelling from a denser to a rarer medium.
2. Draw the sketches to differentiate between plane wavefront and spherical wavefront.

Answer:

Proof of SNELL’S Law:

Consider a plane wavefront (AB) incident on the surface XY. separating two media. Let the secondary wavelets from point (B) reach up to point (C) in lime (t). So draw an arc of length (v₂t) from point A to locate the position of refracted WF. Now we draw a tangent (CD) on this arc where CD represents refracted WF.

Incident ray, refracted ray & the normal arc respectively1 to incident WF. refracted WF and surface XY.

Also, \(\sin \mathrm{i}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{v_1 t}{A C}\) → (1)

and \(\sin r=\frac{A D}{A C}=\frac{v_2 t}{A C}\) → (2)

From (1) and (2)

∴ \(\frac{v_1}{v_2}=\frac{\sin i}{\sin r}\)

Or \(\frac{\mu_2}{\mu_1}=\frac{\sin i}{\sin r}\)

Hence Snell’s law is proved

Question 6.

1. In Young’s double slit experiment, two slits arc I mm apart and the screen is placed 1 m away from the slits. Calculate the fringe width when light of wavelength 500 nm is used.
2. What should be the width of each slit to obtain 10 maxima of the double slit pattern within the central maximum of the single slit pattern?

Answer:

d = 1 mm, D = I m, λ = 500 nm (given)

∴ \(\beta=\frac{\lambda \mathrm{D}}{\mathrm{d}}=\frac{500 \times 10^{-9} \times 1}{10^{-3}} \mathrm{~m}=500 \times 10^{-6} \mathrm{~m}=500 \mu \mathrm{m}\)

2. In single slit diffraction, path diff. = a sinθ ≅ aθ = X ⇒ θ = λ/a

Width of central maxima of single slit = 2λ/a

Width of 10 maxima = 10 x fringe spacing = 10 x λ/6

Width of central maximum of single slit = Width of 10 maxima of double slit

∴ \(\frac{10 \lambda}{d}=\frac{2 \lambda}{a} \Rightarrow a=\frac{d}{5}=0.2 \mathrm{~mm}\)

Question 7. Two harmonic waves of monochromatic light y₁ = a cos ωt and y₂ = a cos(ωt +Φ) are superimposed on each other. Show that the maximum intensity in the interference pattern is four times the intensity due to each slit. Hence write the conditions for constructive and destructive interference in terms of the phase angle Φ.

Answer:

Given, y, = a cos ωt, y, = a cos(ωt + Φ)

Resultant displacement is given as:

y = y₁ +y₂

= a cos ωt + a cos(ωt + Φ)

= a cos ωt + a cos ωt cos Φ – a sin ωt sin Φ

= a cos ωt (1+ cos Φ)- a sin ωt sin Φ

Put R cos θ = a (1 + cos Φ) → (1)

R sin θ = a sin Φ → (2)

By squaring and adding Eqs. (1) and (2), we get

R² = a²(1+cos^2Φ + 2cosΦ) + a²sin^2Φ – 2a²( 1 + cos Φ ) = 4a²cos²Φ/2

∴ \(I=R^2=4 a^2 \cos ^2 \frac{\phi}{2}=4 I_0 \cos ^2 \frac{\phi}{2}\)

1. For constructive interference,

∴ \(\cos \frac{\phi}{2}= \pm 1 \text { or } \frac{\phi}{2}=n \pi \text { or } \phi=2 n \pi, n=0,1,2 \ldots\)

2. For destructive interference,

∴ \(\cos \frac{\phi}{2}=0 \text { or } \frac{\phi}{2}=(2 n+1) \frac{\pi}{2} \text { or } \phi=(2 n+1) \pi, n=0,1,2 \ldots\)

Question 8.

1. If one of two identical slits producing interference in Young’s experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern.
2. What kind of fringes do you expect to observe if white light is used instead of monochromatic light?

Answer:

1. Let the intensity through one of the slits be I₁ =1.

So. intensity of light through the slit covered by glass

I₂ = 0.5I

Maximum intensity \(I_{\max }=\left(\sqrt{I_1}+\sqrt{I_2}\right)^2\)

⇒ \(I_{\mathrm{max}}=(\sqrt{\mathrm{I}}+\sqrt{0.5 \mathrm{I}})^2=2.9 \mathrm{I}\)

Minimum Intensity = \(I_{\min }=\left(\sqrt{I_1}-\sqrt{I_2}\right)^2\)

⇒ \(I_{\min }=(\sqrt{I}-\sqrt{0.5 I})^2=0.086 I\)

Thus ratio of intensities \(\frac{I_{\max }}{I_{\min }}=\frac{2.9}{0.086}=33.8\)

2. If white light is used in place of monochromatic light, then the central fringe will be white and some coloured fringes will be seen adjacent to the central fringe.

Question 9. Explain the following, giving reasons:

1. When monochromatic light is incident on a surface separating two media, the reflected and refracted light both have the same frequency as the incident frequency.
2. When light travels from a rarer to a denser medium, the speed decreases, does this decrease in speed imply a reduction in the energy carried by the wave?
3. In the wave picture of light, the intensity of light is determined by the square of the amplitude of the wave. What determines the intensity in the photon picture of light?

Answer:

1. Reflection and refraction arise through the interaction of incident light with the atomic constituents of matter. Atoms may be viewed as oscillators, which light up the frequency of the external agency (light) causing forced oscillations. The frequency of emitted light by a charged oscillator equals to its freq. of oscillation. Thus, the frequency of scattered light equals the frequency of incident light.
2. No, the energy carried by a wave depends on the amplitude of the wave, not on the speed of
   wave.
3. For a given frequency, the intensity of light in the photon picture is determined by the no. of photons lulling on unit area per unit time.

Question 10. Monochromatic light of wavelength 600 nm is incident from air on a water surface. The refractive index of water is 1.33. Find the

1. Wavelength,
2. Frequency and
3. Speed, of reflected and refracted light.

Answer:

Given: X = 600 nm, \(\mathrm{n}_{\mathrm{w}}=\frac{4}{3}=1.33\)

Frequency of incident ray

⇒ \(c=f \lambda \Rightarrow f=\frac{c}{\lambda}=\frac{3 \times 10^8}{600 \times 10^{-10}}\)

f = 5 x 10¹⁴ Hz

Question 11.

1. Stale two conditions for two light sources to be coherent.
2. Give two points of difference between an interference pattern due to a double-slit and a diffraction pattern due to a single slit.

Answer:

1. Two sources are said to be coherent if-
   • These produce waves of the same frequency with
   • Constant or zero phase difference
2. Interference is the result of the superposition of secondary wavelets from two different slits while diffraction results due to the superposition of secondary wavelets from different parts of the same source slit.
   • In the interference pattern, all maxima are equally bright while in the case of diffraction, maxima are of decreasing intensity.

Question 12. How is the spacing between fringes in a double slit experiment affected if:

1. The slits separation is increased.
2. The colour of light used is changed from red to blue.
3. The whole apparatus is submerged in an oil with a refractive index of 1.2.

Justify your answer in each case

Answer:

Spacing between fringes in a double slit experiment is given by \(\beta=\frac{\lambda \mathrm{D}}{\mathrm{d}}\)

Where, λ => Wavelength of light; d ⇒ Slit separation; D ⇒ Distance between slit and screen

On increasing *d’ fringe width decreases

λ_red > λ_blue. So ‘β’ decreases.

When the whole apparatus is immersed in oil of refractive index 1 .2. the wavelength decreases.

∴ \(\lambda^{\prime}=\frac{\lambda}{1.2}\)

∴ \(\beta^{\prime}=\frac{\lambda^{\prime} \mathrm{D}}{\mathrm{d}}\)= \(\beta^{\prime}=\frac{\beta}{1.2}\)

It means fringe width decreases.

 CBSE Class 12 Physics Chapter 10 Wave Optics Long Questions and Answers

Question 1. Wavefront is a locus of points which vibrates in the same phase. A ray of light is perpendicular to the wavefront. According to Huygens principle, each point of the wavefront is the source of a secondary disturbance and the wavelets connecting from these points spread out in all directions with the speed of the wave. The figure shows a surface XY separating two transparent media. medium- 1 and medium-2. The lines ah and cd represent wavefronts of a light wave\e tra\elling in medium- 1 and incident on XY. The lines of and gh represent wavefronts of the light wa\c in medium -2 after refraction.

(1). Light travels as a

1. Parallel beam in each medium
2. Convergent beam in each medium
3. Divergent beam in each medium
4. Divergent beam in one medium and convergent beam in the other medium

Answer: 1. Parallel beam in each medium

(2). The phases of the light wave at c, d, c and f are Φ_c, Φ_d, Φ_e, and Φ_f respectively. It is given that Φ_c = Φ_f

1. Φ_c can not be equal to Φ_d
2. Φ_d can be equal to Φ_e
3. (Φ_d – Φ_f) is equal to (Φ_c– Φ_e)
4. (Φ_d– Φ_c ) is not equal to (Φ_f – Φ_e)

Answer: 3. (Φ_d – Φ_f) is equal to (Φ_c– Φ_e)

(3). Wavefront is the locus of all points, where the particles of the medium vibrate with the same

1. Phase
2. Amplitude
3. Frequency
4. Period

Answer: 1. Phase

(4). A point source that emits waves uniformly in all directions, produces wavefronts that are

1. Spherical
2. Elliptical
3. Cylindrical
4. Planar

Answer: 1. Spherical

Question 2.

1. Define a wavefront. Using Huygens principle, verify the laws of reflection at a plane Surface
2. In a single slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band? Explain.
3. When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the obstacle. Explain why?

Answer:

1. The wavefront is defined as a surface of constant phase.

(Alternatively: The wavefront is the locus of all points in the same phase).

Let the speed of the wave in the medium be ‘v’

Let the time taken by the wavefront, to advance from point B to point C is ‘τ’

Hence BC = vτ

Let CE represent the reflected wavefront. Distance AE = vτ = BC

Δ AEC and Δ ABC are congruent

∴ ∠ABC = ∠AEC(90°)

AC = AC

AE = BC.

So, ∠BAC = ∠ECA (by corresponding part of congruent triangles)

= ∠i = ∠r (proved)

2. If the width of the slit is made double then the size of the central maxima reduces to half and intensity increases upto four times.

3. This is because of the diffraction of light.

[Alternatively: Light gels diffracted by the tiny circular obstacle and reach the centre of the shadow of the obstacle.]

[Alternatively: There is a maxima, at the centre of the obstacle, in the diffraction pattern produced by it.]

Question 3.

1. Give an expression for path difference in Young’s double slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
2. The intensity at the central maxima in Young’s double-slit experiment is I₀. Find out the intensity at a point where the path difference is \(\frac{\lambda}{6},\frac{\lambda}{4} \text { and } \frac{\lambda}{3}\)

Answer:

1. Conditions for interference of light:

• Both sources of light must be coherent.
• Both sources of light should be monochromatic.

Expression for fringe width in Young’s double slit experiment:

Path difference between the light waves reaching point P from S₁ and S₂

Δx = S₂P -S₁P

Path difference \((\Delta \mathrm{x})=\frac{\mathrm{y}_{\mathrm{n}} \mathrm{d}}{\mathrm{D}}\)

Case (1) Position of bright fringes:

If n^th bright fringe occurs at point P. then the path difference

Δx = nλ

∴ \(\frac{y_n d}{D}=n \lambda \Rightarrow y_n=\frac{n \lambda D}{d} \text { where } n=0,1,2,3, \ldots .\)

y_n ⇒ position of n^th bright fringe on screen from the central bright fringe.

Case (2) Position of dark fringes:

Path difference for n^th dark fringe

Δx = (2n – I )λ/2

⇒ \(\frac{y_n^{\prime} d}{D}=(2 n-1) \lambda/2\)

⇒ \(y_n^{\prime}=\frac{(2 n-1) \lambda D}{2 d} \text { where } n=1,2,3, \ldots .\)

y’_n ⇒ position of n^th dark fringe.

Fringe width:

The distance between two consecutive bright or dark fringes is called fringe width.

fringe width \((\beta)=y_{n+1}-y_n\) (Taking Condition for bright fringe \(y_n=\frac{n{\lambda}D}{\mathrm{d}}\))

⇒ \(\beta=\frac{(n+1)\lambda D}{d}-\frac{n \lambda D}{d}\)

∴ \(\beta=\frac{\lambda D}{d}\)

Intensity distribution curve:

2. As we Know, I = 4I₀ Cos²(Φ/2)

Φ = Phase difference

⇒ \(\phi=\frac{2 \pi}{\lambda} \cdot \Delta x\) (Δx = path diff.)

(1) From, \(\phi=\frac{2 \pi}{\lambda} \cdot \Delta x=\frac{2 \pi}{\lambda} \cdot \frac{\lambda}{6}\)

Φ = π/3 = 60°

So, \(I=4 I_0 \cos ^2 30^{\circ}=4 I_0 \cdot \frac{3}{4}\)

I = 3I₀

(2). From \(\phi=\frac{2 \pi}{\lambda} \cdot \Delta x=\frac{2 \pi}{\lambda} \cdot \frac{\lambda}{4}=\frac{\pi}{2}=90^{\circ}\)

So, \(I=4 I_0 \cos ^2 45^{\circ}=4 I_0 \cdot \frac{1}{2}\)

I = 2 I₀

(3). From, \(\phi=\frac{2 \pi}{\lambda} \cdot \Delta x=\frac{2 \pi}{\lambda} \cdot \frac{\lambda}{3}=\frac{2 \pi}{3}=120^{\circ}\)

So, \(I=4 I_0 \cos ^2 60^{\circ}=4 I_0 \cdot \frac{1}{4}\)

I = I₀

Question 4.

1. State the essential conditions for diffraction of light.
2. Explain the diffraction of light due to a narrow single slit and the formation of a pattern of fringes on the screen.
3. Find the relation for the width of central maximum in terms of wavelength ‘λ’ width of slit ‘a’, and separation between slit and screen ‘D’.
4. If the width of the slit is made double the original width, how does it affect the size and intensity of the central band?

Answer:

1. The wavelength of light should be comparable to the site of the obstacle,

2. Suppose a plane wavefront is incident on a slit AH (of width b), every part of the exposed part of the plane wavefront (i.e., every part of the slit) acts as a source of secondary wavelets spreading in all directions.

The diffraction is obtained on a screen placed at a large distance. (In practice, this condition is achieved by placing the screen at the focal plane of a converging lens placed to alter the slit).

• The diffraction pattern consists of a central bright fringe (central maxima) surrounded by dark and bright lines (called secondary minima and maxima).
• At point 0 on the screen, the central maxima is obtained. The wavelets originating from points A and B meet in the same phase at this point, hence at 0, intensity is maximum.

Secondary minima

For obtaining n^th secondary minima at P on the screen, the path difference between the diffracted waves Δ = b sinθ = nλ (n = 0,1, 2, … )

Angular position of n^th secondary minima

⇒ \(\sin \theta \simeq 0=\frac{n {\lambda}}{b}\)

Distance of nth secondary minima from central maxima

⇒ \(x_n=D \cdot \theta=\frac{n \lambda D}{b}=\frac{n \lambda f}{b}\)

where D = distance between slit and screen.

f ≅ D = Focal length of converging lens.

Secondary maxima:

For nth secondary maxima at P on the screen.

Path difference. \(\Delta=b \sin \theta =(2 n+1) \frac{\lambda}{2}\); where n = 1,2,3….

Angular position of n^th secondary maxima

∴ \(\sin \theta \simeq \theta=\frac{(2 n+1) \lambda}{2 b}\)

Distance of nth secondary maxima,from central maxima

∴ \(x_n=D \cdot \theta=\frac{(2 n+1) \lambda D}{2 b}=\frac{(2 n+1) \lambda f}{2 b}\)

3. The Central Maximum:

The width of the central maximum is simply the distance between the 1^st order minima from the centre of the screen on both sides of the centre.

The position of the minima given by ‘y’ (measured from the centre of the screen) is:

The position of the minima given by ‘y’ (measured from the centre of the screen) is:

∴ \(\tan \theta \simeq \theta=\frac{y}{D}\)

For small θ, sinθ ≅ θ

λ = bsinθ – bθ

⇒ \(\theta=\frac{y}{D}=\frac{\lambda}{b}\)

⇒ \(y=\frac{\lambda D}{b}\)

The width of the central maximum is simply twice this value width of central maximum = \(2 \frac{\lambda D}{b}\)

angular width of central maximum = 2θ = \(2 \frac{\lambda}{b}\)

4. If the width of the slit is made double then the size of the central maxima reduces to half and intensity increases upto four times.

 CBSE Class 12 Physics Chapter 9 Ray Optics And Optical Instruments Multiple Choice Questions And Answers

Question 1. For a thin convex lens when the height of the object is double its image, its object distance is equal to ________.

1. f
2. 2f
3. 3f
4. 4f

Answer: 3. 3f

⇒ \(m=\frac{f}{f-u}\)

⇒ \(-\frac{1}{2}=\frac{f}{f-(-u)}\)

⇒ -f-u = 2f

∴ |u| = 3f

Read and Learn More Important Questions for Class 12 Physics with Answers

Question 2. Which of the following is responsible for the glittering of diamonds?

1. Interference
2. Diffraction
3. Total internal reflection
4. Refraction

Answer: 3. Total internal reflection

Question 3. The focal length of a thin lens made from the material of a refractive index of 1.5 is 20 cm. When it is placed in a liquid of refractive index 4/3 its focal length will be _________ cm.

1. 80.00
2. 60.25
3. 45.48
4. 78.23

Answer: 4. 45.48

⇒ \(\frac{f_1}{f_a}=\left(\frac{_a \mu_g-1}{_l \mu_z-1}\right)\)

⇒ \(\frac{f_l}{20}=\frac{(1.5-1)}{\left(\begin{array}{l}
1.5 \\
1.33
\end{array}\right)}\)

∴ f_l = 78.23 cm

Question 4. The radii of curvature of both sides of a convex lens are 15 cm and if the refractive index of the material of the lens is 1.5. Then the focal length of the lens in air is _________ cm.

1. 10
2. 15
3. 20
4. 30

Answer: 2. 15

⇒ \(\frac{1}{f_a}=\left(_a\mu_g-1\right)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)

⇒ \(\frac{1}{f_a}=\frac{1}{2}\left(\frac{1}{15}-\frac{1}{-15}\right)\)

⇒ \(\frac{1}{f_a}=\frac{1}{2} \times \frac{2}{15}\)

∴ f_a = 15 cm

Question 5. If the tube length of the astronomical telescope is 105 cm and the magnifying power is 20 for a normal setting, then the focal length of the objective is ________ cm.

1. 10
2. 20
3. 25
4. 100

Answer: 4. 100

Question 6. An object is placed at a distance of 25 cm on the axis of a concave mirror having a focal length of 20 cm. What will be the lateral magnification of an image?

1. 4
2. 2
3. -4
4. -2

Answer: 3. -4

⇒ \(m=\frac{f}{f-u}\)

⇒ \(\frac{-20}{-20-(-25)}=\frac{-20}{5}\)

∴ m = -4

Question 7. The depth of a filled well is II m and the refractive index of water is 1.33. If viewed normally from the top, by how much height would the bottom of the well appear to be shifted up?

1. 2.73 m
2. 11 m
3. 4.13 m
4. 1.37 m

Answer: 1. 2.73 m

⇒ \(h=\frac{H}{\mu}=\frac{11}{4} \times 3=\frac{33}{4}\)

Vertical shifted

⇒ \(H-h=11-\frac{33}{4}\)

∴ \(\frac{44-33}{4}=\frac{11}{4}=2.73 \mathrm{~m}\)

Question 8. In an optical fibre, the refractive index of the material of the core is _______ that of the cladding.

1. Less than
2. Higher than
3. Equal to
4. Half

Answer: 2. Higher than

Question 9. The lower half of the concave mirror’s reflecting surface is covered with an opaque (non – reflective) material. The intensity of the image of an object placed in front of the mirror becomes ________.

1. Four times
2. Half
3. One fourth
4. Double

Answer: 2. Half

Question 10. If the focal length of the converging lens is 0.25 m then the power of this lens is _____ dioptre.

1. +2
2. -4
3. +4
4. -2

Answer: 3. +4

∴ \(P=\frac{1}{f}=\frac{1}{0.25}=4 D\)

 CBSE Class 12 Physics Chapter 9 Assertion And Reason

For question numbers 1 to 6 two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (1), (2), (3) and (4) as given below.

1. Both A and R are true and R is the correct explanation of A
2. Both A and R are true but R is NOT the correct explanation of A
3. A is true but R is false
4. A is false and R is also false

Question 1. Assertion: Critical angle is minimum for violet colour.

Reason: Because critical angle \(\theta_c=\sin ^{-1}\left(\frac{1}{\mu}\right) \text { and } \mu \propto \frac{1}{\lambda} \)

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 2. Assertion: Within a glass slab a double convex air bubble is formed. This air bubble behaves like a converging lens.

Reason: The refractive index of air is more than the refractive index of glass.

Answer: 4. A is false and R is also false

Question 3. Assertion: A beam of white light gives a spectrum on passing through a hollow prism.

Reason: The speed of light outside the prism is different from the speed of light inside the hollow prism.

Answer: 4. A is false and R is also false

Question 4. Assertion: The microscope magnifies the image.

Reason: Angular magnification for images is more than one in the microscope.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 5. Assertion: Spherical aberration occurs in lenses of larger aperture.

Reason: The two types of rays, paraxial and marginal rays focus at different points.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 6. Assertion: The angle of minimum deviation for a prism is lesser for red light than that for blue light.

Reason: The refractive index of the material of a prism for blue light is greater than that for red light.

Answer: 1. Both A and R are true and R is the correct explanation of A

 CBSE Class 12 Physics Chapter 9 Short Question And Answers

Question 1. Light from a point source in the air falls on a convex spherical glass surface with a refractive index of 1.5 and a radius of curvature of 20 cm. The distance of the light source from the glass surface is 100 cm. At what position is the image formed?

Answer:

Given: 1 = 1, 2 = 1.5, R = 20cm. u = -100 cm

Form \(\frac{\mu_2}{v}-\frac{\mu_1}{u}=\frac{\mu_2-\mu_1}{R} \Rightarrow \frac{1.5}{v}-\frac{1}{-100}=\frac{0.5}{20}\)

⇒ \(\frac{1.5}{v}=\frac{5}{200}-\frac{1}{100}=\frac{3}{200} \text { or } v=100 \mathrm{~cm}\)

Question 2. A beam of light converges at a point P. A lens is placed in the path of the beam at a distance of 25 cm from P. The final image is formed at infinity. Calculate the power of the lens.

Answer:

So, u = 25 cm, v = ∞

⇒ \(\mathrm{f}=-25 \mathrm{~cm}=-\frac{25}{100} \mathrm{~m}=-\frac{1}{4} \mathrm{~m}\)

∴ \(P=\frac{l}{f}=-4 D\)

Question 3. A ray of light falls on a transparent sphere of μ = √3 at an angle of incidence 60° with the diameter AB of the sphere having centre C. The ray emerges from the sphere parallel to the line AB. Find the angle of emergence.

Answer:

⇒ \(\mu=\frac{\sin i}{\sin r_1}\)

⇒ \(\sqrt{3}=\frac{\sin 60^{\circ}}{\sin r_1}\)

⇒ \(\sin r_1=\frac{\sqrt{3}}{2} \times \frac{1}{\sqrt{3}}\)

r₁ = 30°

i.e. r₁ = r₂ = 30° so, e = 60° [angle of emergence]

Question 4.

1. Explain briefly how the focal length of a convex lens changes with an increase in the wavelength of incident light.
2. Explain briefly how the focal length of a convex lens changes when it is immersed in water. The refractive index of the material of the lens is greater than that of water.

Answer:

1. From \(\mu=\frac{\mathrm{c}}{\mathrm{v}}=\frac{\mathrm{c}}{\mathrm{v \lambda}}\)

Here, refractive index \(\mu \propto \frac{1}{\lambda}\)

So, (.t of a lens increases with the decrease in wavelength of the incident light.

From \(\frac{1}{f}=(\mu-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)

We can say focal length will increase with the increase in wavelength and vice versa.

2. From, \(\frac{1}{f}=\left(\frac{\mu_2}{\mu_1}-1\right)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\) 2 (lens) = 1.5, 1 (Water) = 1.33

⇒ \(\frac{1}{f}=\left(\frac{1.5}{1.33}-1\right)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\) When lens placed in water

Clearly \(\left(\frac{\mu_2}{\mu_1}\right)\) decreases which means focal length increases.

Question 5. A ray PQ incident normally on the refracting face BA is refracted in the prism BCA made of material of refractive index 1.5. Complete the path of the ray through the prism. From which face will the ray emerge?

Answer:

Refractive index (μ) = 1.5 (given)

Ray PQ will go straight in ΔBAC as it falls normally on the surface BA. From the condition of TIR.

⇒ \(\sin \mathrm{i}_C=\frac{1}{\mu}=\frac{1}{1.5}=\frac{2}{3}=0.66\)

or i_c = 42° (∵ sin 42° = 0.66)

⇒ \(\frac{\sin i}{\sin r}=\frac{\mu_2}{\mu_1}=\frac{2}{3}\)

or \(\frac{\sin 30^{\circ}}{\sin r}=\frac{2}{3}\)

or sin r = 0.75

or r = 48.5° (∵ sin 48.5° = 0.75)

So ray PQ will emerge from surface AC at an angle = 48.5°

Question 6. A beam of light converges at a point P. Draw ray diagrams to show where the beam will converge if

1. A convex lens, and
2. A concave lens is kept in the path of the beam.

Answer:

Question 7. A coin is placed inside a denser medium. Why does it appear to be raised? Obtain an expression for the height through which the object appears to be raised in terms of the refractive index of the medium and real depth.

Answer:

Because of Refraction, it appears to be raised.

⇒ \(\Delta \mathrm{OMP} \rightarrow \sin i=\frac{\mathrm{MP}}{\mathrm{OM}}\)

⇒ \(\Delta \mathrm{XMP} \rightarrow \sin r=\frac{\mathrm{MP}}{\mathrm{XM}}\)

So, \(\text { So, }{ }_d \mu_r=\frac{\sin i}{\sin r}=\frac{X M}{O M}\)

If M and P are closer, then XM ≅ XP = h’ (Apparent depth), OM = OP = H (Actual Depthdepth)

⇒ \({ }_d \mu_r=\frac{h^{\prime}}{h}\)

⇒ \(\frac{1}{{ }_r \mu_d}=\frac{h^{\prime}}{h}\)

∴ \(h^{\prime}=\frac{h}{\mu}\) (\(\left[d \mu_r=\frac{1}{\mu_d}=\frac{1}{_r\mu_1}\right]\))

Thus the height (vertical shift) through which, the object appears to be raised

∴ \(\Delta=h-h^{\prime}=h\left(1-\frac{1}{\mu}\right)\)

Question 8. Under what conditions does the phenomenon of total internal reflection lake place? Draw a ray diagram showing how a ray of light deviates by 90° after passing through a right-angled isosceles prism.

Answer:

Conditions:

1. The light must move from a denser to a rarer medium.
2. The angle of incidence must be greater than the critical angle.

Question 9. State, with the help of a ray diagram, the working principle of optical fibres. Write one important use of optical fibres.

Answer:

Working principle of optical fibres: Optical fibres are extensively used for transmitting audio and video signals in the form of light from one end to another based on multiple total internal reflections at the interface of inner and outer layers which are known as core and cladding.

Use: Used in visual examination of Internal organs like the stomach and intestine by the endoscopy in medical Science

Question 10. Which two aberrations do objectives of refracting telescope suffer from? How are these overcome in reflecting telescopes?

Two Aberrations: Spherical aberration & chromatic aberration. Spherical aberration in mirrors is corrected by using parabolic mirrors and in lenses it is corrected by using a lens with a small aperture or one side plane.

Chromatic aberration is reduced by using an achromatic combination of lenses in which materials with differing dispersive properties arc assembled to form a compound lens.

Question 11. A compound microscope consists of an objective lens of focal length 2 cm and an eyepiece of focal length 6.25 cm separated by a distance of 15 cm. How far from the objective should an object be placed to obtain the final image at the least distance of distinct vision (25 cm)? Calculate the magnifying power of the microscope.

Answer:

f₀ = 2cm. f_e = 6.25 cm. d = 15 cm. D = 25 cm. v_e = -25 cm

⇒ \(\frac{1}{f_e}=\frac{1}{v_e}-\frac{1}{u_e} \Rightarrow \frac{1}{6.25}=\frac{1}{-25}-\frac{1}{u_e} \Rightarrow u_e=-5 \mathrm{~cm}\)

So. the image distance for the objective lens

v₁ = d – u_e = 15 – 5 = 10cm

Now again

⇒ \(\frac{1}{f_0}=\frac{1}{v_0}-\frac{1}{u_0} \Rightarrow \frac{1}{2}=\frac{1}{10}-\frac{1}{u_0} \Rightarrow u_0=-2.5 \mathrm{~cm}\)

Magnifying Power

⇒ \(m=\frac{-v_0}{u_0}\left(1+\frac{D}{f_c}\right)=\frac{10}{2.5}\left(1+\frac{25}{6.25}\right)\)

m = 20

Question 12.

1. An object approaches a converging lens with a uniform speed of 5 m/s and slops at the focus. How- will the image move for the lens? Specify its nature.
2. In a simple microscope, a convex lens of focal length 5 cm is used. Calculate the magnifying power when the object is placed at the focus of the lens.
3. What is the power of a biconvex lens of refractive index n₂ dipped in a liquid of refractive index n₁? where n₁ < n₂?

Answer:

1. Moves away from the lens with a non-uniform speed.

For example: If f = 20 m,

u = -50m. -45m, -40m. -34m

v = 33.3m, 36m. 40m, 46.7m [by using lens formula]

2. \(m=\frac{D}{f}=\frac{25}{5}=5\)

The lens behaves as a convex lens

⇒ \(\mathrm{P}=\frac{1}{\mathrm{f}}=\left(_1\mathrm{n}_2-1\right)\left(\frac{1}{\mathrm{R_1}}-\frac{1}{\mathrm{R}_2}\right)\)

⇒ \(P=\left(\frac{n_2}{n_1}-1\right)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)

₁n₂ < _an₂ (∵ n₁ can not be less than 1 )

So. Focal length will increase. power will decrease.

Question 13. Draw a labelled ray diagram of a refracting telescope. Deduce an expression of magnifying power of it. Write two main limitations of a refracting-type telescope or a reflecting-type telescope.

Answer:

Refracting Telescope:

Refracting type telescope consists of an objective lens of large aperture and large focal length whereas an eyepiece is of small aperture and small focal length.

Magnifying Power:

It is the ratio of visual angle substandard by the final image at the eye to the visual angle subtended by an object.

⇒ \(M=\frac{\beta}{\alpha} \quad\left\{\begin{array}{l}
\text { if } \alpha \text { and } \beta \text { are very small } \\
\alpha \approx \tan \alpha \text { and } \beta \approx \tan \beta
\end{array}\right.\)

⇒ \(M=\frac{\tan \beta}{{tan} \alpha} \Rightarrow M=\frac{\left(\frac{A^{\prime} B^{\prime}}{O_2 B^{\prime}}\right)}{\left(\frac{A^{\prime} B^{\prime}}{O_1 B^{\prime}}\right)} ⇒ M=\frac{O_1 B^{\prime}}{O_2 B^{\prime}}=\frac{-f_0}{u_e}\)

⇒ \(M=\frac{-f_0}{u_e}\) (1)

1. When the final image is formed at least a distance of distinct Vision (V_e = D)

Applying lens formula for eyepiece:

⇒ \(\frac{1}{f_e}=\frac{1}{v_e}-\frac{1}{u_e} \quad\left\{\begin{array}{l}
\text { applying sign convention } \\
v_e=-D . \quad u_e=-u_e
\end{array}\right.\)

⇒ \(\frac{1}{f_e}=-\frac{1}{D}+\frac{1}{u_e} \Rightarrow \frac{1}{u_e}=\frac{1}{f_e}+\frac{1}{D} \Rightarrow \frac{f_0}{u_e}=f_0\left(\frac{1}{f_e}+\frac{1}{D}\right) \Rightarrow \frac{f_0}{u_e}=\frac{f_0}{f_e}\left(1+\frac{f_e}{D}\right)\)

Hence magnifying power from eq (1)

∴ \(M=-f_0\left[\frac{1}{f_e}+\frac{1}{D}\right]\)

2. When the final image is formed at infinity (u_e = f_e )

From eq. (i)

∴ \(M=\frac{-\mathrm{f}_0}{\mathrm{f}_e}\)

Drawbacks of refracting telescope:

1. A defect of chromatic aberration occurs in refracting-type telescopes.
2. It has a small resolving power

Question 14.

1. Draw a ray diagram depicting the formation of the image by an astronomical telescope in normal adjustment.
2. You are given the following three lenses. Which two lenses will you use as an eyepiece and as an objective to construct an astronomical telescope? give reason.

Answer:

2. ‘L₁‘ is used for an objective as it has the largest focal length which is needed, \(M_0=\frac{f_0}{f_e}\) for better-magnifying power. ‘L₃‘ is Used for an eyepiece to get better angular magnification, as from \(M_{0}=\frac{f_{0}}{f_e}\) least f_e is needed.

Question 15.

1. A convex lens of focal length 30 cm is in contact with a concave lens of focal length 20 cm. Find out if the system is converging or diverging.
2. Obtain the expression for the angle of incidence of a ray of light, which is incident on the face of a prism of refracting angle A so that it suffers total internal reflection at the other face. (Given, the refractive index of the glass of the prism is μ.)

Answer:

1. Focal length of convex lens f₁ = 30 cm

the focal length of the concave lens f₂ = -20 cm

Equivalent focal length of combination

⇒ \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2} \Rightarrow \frac{1}{f}=\frac{1}{30}-\frac{1}{20} \Rightarrow \frac{1}{f}=-\frac{1}{60} \Rightarrow f =-60 \mathrm{~cm}\)

The system is diverging.

2. For total internal reflection.

⇒ \(\sin i_c=\frac{1}{\mu}\)

For Prism we know that

r₁ + r₂ = A and r₂ = i_c

∴ r₁ = A -i_c

Applying Snell’s law at point ‘Q’

∴ \(\frac{\sin i}{\sin f_i}=\mu\)

sin i = μ sin r₁ ⇒ sin i = μ sin (A- i_c)

i = sin^-1 |μ sin-(A-i_c)|

Question 16.

1. Name the phenomenon on which the working of an optical fibre is based.
2. Draw a labelled diagram of an optical fibre and show how light propagates through the optical fibre using this phenomenon.

Answer:

1. Total internal reflection (TIR)

Question 17.

1. A screen is placed at a distance of 100 cm from an object. The image of the object is formed on the screen by a convex lens for two different locations of the lens separated by 20 cm. Calculate the focal length of the lens used.
2. A converging lens is kept coaxially in contact with a diverging lens with equal focal length. What is the focal length of the combination?

Answer:

1. For the first position of the lens, we have

∴ \(\frac{1}{f}=\frac{1}{y}-\frac{1}{(-x)}\) → (1)

For the second position of the lens, we have (2)

⇒ \(\frac{1}{f}=\frac{1}{y-20}-\frac{1}{[-(x+20)]}\) →(2)

From (1) and (2)

⇒ \(\frac{1}{y}+\frac{1}{x}=\frac{1}{(y-20)}+\frac{1}{(x+20)} \Rightarrow \frac{x+y}{x y}=\frac{(x+20)+(y-20)}{(y-20)(x+20)}\)

∴ xy = (y – 20) (x + 20) = xy – 20 x + 20 y- 400

∴ x – y = -20

Also, x + y = 100

x= 40 cm and y = 60 cm

∴ \(\frac{1}{f}=\frac{1}{60}-\frac{1}{-40}=\frac{2+3}{120}=\frac{5}{120}\)

∴ f = 24 cm

or

Distance between the image (screen) and the object, D = 100 cm.

Distance between two locations of the convex lens, d = 20cm

Focal length (f) = \(=\frac{D^2-d^2}{4 D}=\frac{(100)^2-(20)^2}{4 \times 100}\)

f = 24 cm.

2. \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{\left(-f_2\right)}=\frac{1}{f_1}-\frac{1}{f_2}\)

⇒ [/altex]\frac{1}{f}=\frac{f_2-f_1}{f2 f_1}[/latex]

∴ \(f=\frac{f_2 f_1}{f_2-f_1}\)

Question 18.

1. Monochromatic light of wavelength 589 nm is incident from air on a water surface. If μ for water is 1.33, find the refracted light’s wavelength, frequency and speed.
2. A double convex lens is made of glass with a refractive index of 1.55, with both faces of the same radius of curvature. Find the radius of curvature required, if the focal length is 20 cm.

Answer:

1. \(\lambda_{\text {air }}=589 \mathrm{~nm}, \mu_{\text {water }}=1.33\) (Given)

For water, \(\lambda_{w a t e r}, \frac{\mu_n}{\mu_a}=\frac{\lambda_a}{\lambda_n} \Rightarrow \lambda_w=\frac{589}{1.33}\)

∴ w = 442.8nm

Frequency of light remains constant.

Velocity, \(v=\frac{c}{\mu}=\frac{3 \times 10^8}{1.33}=2.25 \times 10^8 \mathrm{~m} / \mathrm{s}\)

2. From \(\frac{1}{f}=\left(\mu_{21}-1\right)\left[\frac{1}{R_1}-\frac{1}{R_2}\right] \quad\left\{\begin{array}{l}
\text { Using sign Convention } \\
R_1=+R \quad \text { for equi convex lens } \\
R_2=-R
\end{array}\right.\)

⇒ \(\frac{1}{f}=(1.55-1)\left[\frac{1}{R}-\left(-\frac{1}{R}\right)\right]\)

∴ \(\frac{1}{r}=(.55)\left[\frac{2}{R}\right]=\frac{1.1}{R} \Rightarrow \frac{1}{20}=\frac{1.1}{R} \Rightarrow R=1.1 \times 20=22 \mathrm{~cm}\)

Question 19.

1. A triangular prism with a refracting angle of 60° is made of a transparent material of refractive index 2/√3.
2. A ray of light is incident normally on the face AB as shown in the figure. Trace the path of the ray as it passes through the prism and calculate the angle of emergence and angle of deviation.

Answer:

Given: ∠A = 60°, ∠i = 0°

At M: \(\sin \mathrm{i}_{\mathrm{C}}=\frac{1}{\mu}=\frac{\sqrt{3}}{2}=\sin 60^{\circ}\)

∴ i_c = 60°

So the ray PQ after refraction from the face AC grazes along AC.

∴ ∠e = 90°

From ∠i = ∠e = ∠A + ∠δ

or 0° + 90° = 60° + ∠δ

∴ δ = 90° – 60° = 30°

Question 20.

1. What is total internal reflection? Under what conditions does it occur?
2. Find a relation between critical angle and refractive index.
3. Name one phenomenon which is based on total internal reflection

Answer:

The complete reflection of a light ray at the boundary of two media, when the ray is going from a denser to a rarer medium is called TIR.

Condition:

1. Light rays must pass from a denser to a rarer medium
2. the angle of incidence must be greater than the critical angle, (i > i_c).

In the above Ray Ao goes from denser (say water) to rarer (say air) medium, So using Snell’s law, \(\frac{\sin i}{\sin r}=\frac{\mu_2}{\mu_1}\)

or \(\frac{\sin i_c}{\sin 90^{\circ}}=\frac{\mu_2}{\mu_1}\) [Here, angle of incidence = ic and angle of refraction = 90°]

If refractive index of rarer medium = 1 (i.e. 2 = 1)

or \(\sin i_c=\frac{1}{\mu_1}=\frac{1}{\mu}\) = (∵ \(\))

3. Mirage or Brilliance of diamond.

Question 21. In the following diagram, an object ‘O’ is placed 15 cm in front of a convex lens L₁ of focal length 20 cm and the final image is formed at ‘I’ at a distance of 80 cm from the second lens L₂. Find the focal length of the lens L₂.

Answer:

For Lens L₁: \(\frac{1}{v_1}-\frac{1}{u_1}=\frac{1}{f_1} \Rightarrow \frac{1}{v_1}=\frac{1}{f_1}+\frac{1}{u_1}\)

⇒ \(\frac{1}{v_1}=\frac{1}{20}+\frac{1}{-15}\)

v₁ – 60 cm

Now image formed (v₁) acts as an object for L₂.

For lens L2: \(\frac{1}{v_2}-\frac{1}{u_2}=\frac{1}{f_2} \Rightarrow \frac{1}{80}+\frac{1}{75}=\frac{1}{f_2} \Rightarrow \frac{1}{f_2}=\frac{31}{1200}\)

∴ \(\mathrm{f}_2=\frac{1200}{31} 38.71 \simeq 39 \mathrm{~cm}\)

Question 22. Describe the construction of a compound microscope. Derive an expression for its total magnification. Draw a ray diagram for the formation of an image by a compound microscope.

Answer:

Compound Microscope: Figure shows a ray diagram of a compound microscope. It consists of two convex lenses one nearer to the object is known as the objective and the other closest to the eye is the eyepiece lens. Here objective lens is of small focal length (f₀) and small aperture whereas the eyepiece is also of small focal length but larger than the objective lens and relatively large aperture

The image A’ is formed by the objective lens L₀ of object AB and the final image is A “B’.

Magnifying power (M) = \(\frac{\text { Angle subtended by the final image at eye }}{\text { Angle subtended by the object when it is placed at the least distance of distinct vision at eye }}\)

⇒ \(M=\frac{\beta}{\alpha} \quad\left\{\begin{array}{l}
\text { if } \alpha \text { and } \beta \text { are very smill. then } \\
\alpha=\tan \alpha \text { and } \beta=\tan \beta
\end{array}\right.\)

⇒ \(M=\frac{\tan \beta}{\tan \alpha}\)

∴ \(M=\frac{\left(\frac{A^{\prime \prime} B^{\prime \prime}}{D}\right)}{\left(\frac{A B}{D}\right)}\) = \(M=\frac{A^{\prime \prime} B^{\prime \prime}}{A B}\)

⇒ \(M=\frac{A^{\prime \prime} B^{\prime \prime}}{A^{\prime} B^{\prime}} \times \frac{A^{\prime} B^{\prime}}{A B} \Rightarrow M=m_e \times m_o \quad\left\{\begin{array}{l}
m_0=\frac{-v_0}{u_0} \\
m_c=\frac{v_e}{u_e}
\end{array}\right.\)

⇒ \(\mathrm{M}=\frac{-\mathrm{v}_{\mathrm{o}}}{\mathrm{u}_{\mathrm{o}}} \times \frac{\mathrm{v}_{\mathrm{c}}}{\mathrm{u}_{\mathrm{c}}}\) (1)

Applying lens Formula for eyepiece \(\)

⇒ \(\frac{1}{f_e}=\frac{1}{v_e}-\frac{1}{u_e} \quad\left\{\begin{array}{l}
v_e=-D \\
u_e=-u_e
\end{array}\right.\)

∴  \(\frac{1}{f_e}=-\frac{1}{D}+\frac{1}{u_e} \Rightarrow \frac{D}{f_e}=-1+\frac{D}{u_e}\) = \(\frac{\mathrm{D}}{\mathrm{u}_{\mathrm{e}}}=1+\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\) (2)

1. When the final image is formed at least the distance of district vision (V_e = -D)

⇒ \(M=\frac{-V_0}{u_0} \times \frac{D}{U_e}\)

∴ \(M=\frac{-V_0}{u_0}\left(1+\frac{D}{f_e}\right)\) → (3)

2. When the final image is formed at infinity (u_e = f_e)

∴ \(M=\frac{{-v_0}}{u_0} \times \frac{D}{1}\) (4)

Question 23.

1. For a glass prism (μ = √3) the angle of minimum deviation is equal to the angle of the prism. Calculate the angle of the prism.
2. Draw a ray diagram when the incident ray falls normally on one of the two equal sides of a right-angled isosceles prism having refractive index μ = √3.

Answer:

Given. δ_m = A

From \(\mu=\frac{\sin \left(\frac{A+\delta_m}{2}\right)}{\sin (A / 2)}\) = \(\frac{\sqrt{3}}{1}=\frac{\sin \left(\frac{A+A}{2}\right)}{\sin (A / 2)}=\frac{\sin A}{\sin (A / 2)}\)

⇒ \(\sqrt{3}=\frac{2 \sin (A / 2) \cos (A / 2)}{\sin (A / 2)}\) = \(\frac{\sqrt{3}}{2}=\cos \mathrm{A} / 2\)

⇒ \(\cos 30^{\circ}=\cos (\mathrm{A} / 2) \Rightarrow 30^{\circ}=\mathrm{A} / 2\)

∴ A = 60°

2. Given μ = √3 (Prism)

For total internal reflection, angle of incidence (i) > critical angle (i_c)

i.e. i > i_c

or sin i > sin i_c

or \(\sin i>\frac{1}{\mu}\)

or \(\sin 45^{\circ}>\frac{1}{\mu}\)

or μ > 2

Hence, ray PQ suffers TIR and goes along path TS.

Question 24.

1. Draw a schematic diagram of a reflecting telescope
2. Slate the advantages of reflecting telescope over refracting telescope.

Answer:

Schematic diagram of a reflecting telescope (Cassegrain).

1. Reflecting telescopes do not suffer from chromatic aberration.
2. The intensity of light is higher in the case of a reflecting telescope.
3. Reflecting telescope’s mirrors arc easier to mount.
4. Manufacturing of mirrors is cheaper compared to lenses.

Question 25. A symmetric biconvex lens of radius of curvature R and made of glass of refractive index 1.5, is placed on a layer of liquid placed on top of a plane mirror as shown in the figure. An optical needle with its lip on the principal axis of the lens is moved along the axis until its real, inverted image coincides with the needle itself. The distance of the needle itself. The distance of the needle from the lens is measured to be x. On removing the liquid layer and repeating the experiment, the distance is found to be y. Obtain the expression for the refractive index of the liquid in terms of x and y.

Answer:

Let μ₁ denote the refractive index of the liquid. When the image of the needle coincides with the needle itself; its distance from the lens, equals the relevant focal length.

With a liquid layer present, the given set-up is equivalent to a combination of the given (convex) lens and a concave plane or piano concave ‘liquid ‘lens’.

We have \(\frac{1}{f}=(\mu-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)

and \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\)

⇒ \(\frac{1}{x}=\frac{1}{f_l}+\frac{1}{y}\)

as per the given data, we then have

⇒ \(\frac{1}{r_2}=\frac{1}{y}=(1.5-1)\left[\frac{1}{R}-\left(-\frac{1}{R}\right)\right]=\frac{1}{R} = \left\{\begin{array}{l}
\frac{1}{y}=\frac{1}{R}=\frac{1}{f_2} \\
f=x
\end{array}\right\}\)

∴ \(\frac{1}{x}=\left(\mu_1-1\right)\left(-\frac{1}{R}\right)+\frac{1}{y}=\frac{-\mu_1}{y}+\frac{2}{y}\)

∴ \(\frac{\mu_1}{y}=\frac{2}{y}-\frac{1}{x}=\left(\frac{2 x-y}{x y}\right) \text { or } \mu_1=\left(\frac{2 x-y}{x}\right)\)

Question 26. The figure shows a ray of light falling normally on the face AB of an equilateral glass prism having refractive index \(\frac{3}{2}\), placed in water of refractive index \(\frac{4}{3}\) Will this ray suffer total internal reflection on striking the face AC?

Answer:

The angle of incidence, of the ray, on striking the face AC is i = 60° (as in figure)

Also. the relative refractive index of glass, concerning the surrounding water, is \(\mu_{\mathrm{r}}=\frac{3 / 2}{4 / 3}=\frac{9}{8}\)

Also \(\sin \mathrm{i}=\sin 60^{\circ}=\frac{\sqrt{3}}{2}=\frac{1.732}{2}=0.866\)

For total internal reflection, the required critical angle, in this case, is given by.

⇒\(sin \mathrm{i}_{\mathrm{C}}=\frac{1}{\mu}=\frac{8}{9} \simeq 0.89\)

∴ i < ic

Hence the ray would not suffer total internal reflection on striking the face AC.

[The student may just write the two conditions needed for total internal reflection without analysis of the given case]

Question 27. Establish a relation between focal length, distance of object and distance of image in concave mirror.

Answer:

u ⇒ distance between pole and object

v ⇒ distance between pole and image

f ⇒ focal length

In ΔA’FB’ and ΔRFQ

∠QFR = ∠A’FB’ and ∠A’B’ F = ∠RQF = 90°

∴ ΔA’FB’- ΔRFQ. so

\(\frac{A^{\prime} B^{\prime}}{Q R}=\frac{F B^{\prime}}{Q F} \Rightarrow \frac{A^{\prime} B^{\prime}}{A B}=\frac{F B^{\prime}}{Q F}\) (1) (from QR = AB)

Similarly ΔABC ∼ ΔA’B’c, hence

⇒ \(\frac{A^{\prime} B^{\prime}}{A B}=\frac{B^{\prime} C}{B C}\) → (2)

From eq (1) and(2)

∴ \(\frac{\mathrm{FB}^{\prime}}{\mathrm{QF}}=\frac{\mathrm{B}^{\prime} \mathrm{C}}{\mathrm{BC}}\)

Point Q is very close to P, Hence ⇒ QF ≈PF

⇒ \(\frac{P B^{\prime}-P F}{P F}=\frac{P C-P B^{\prime}}{P B-P C}\)

Applying sign convention, PB’ = -v, PF = -f, PC = -2f and PB = -u-0

⇒ \(\frac{-v-(-f)}{-f}=\frac{-2 f-(-v)}{u-(-2 f)}\)

On solving, uv – uf = vf

divide by uvf

∴ \(\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{\mathrm{l}}{\mathrm{v}}\)  (This is mirror’s equation)

Question 28. Refractive indices of the given prism material for Red, Blue and Green colours arc 1 .39. 1 .48 and 1 .42 respectively. Trace the path of rays through the prism.

Answer:

For TIR

i > i_c

sin i > sin i_c

⇒ \(\sin i>\frac{1}{\mu}\)

cosec i < μ

(μ_R = 1 .39, μ_G = 1 .42, μ_B = 1 .48

Now → cosec 45° = √2 = 1 .414

So, μ_R < cosec i [Red colour will refract]

μ_B > cosec i [Blue colour will be internally reflected]

μ_G > cosec i [Green colour will be internally reflected]

Question 29. Two prisms ABC and DBC are arranged as shown in the figure

The Ctritical angles for the two prisms concerning air are 41.1 and 45 respectively. Trace the path of the ray through the combination.

Answer:

Question 30.

1. An object is placed in front of a converging lens. Obtain the conditions under which the magnification produced by the lens is
   1. Negative and
   2. Positive.
2. A point object is placed at 0 in front of a glass sphere. Show the formation of the image by the sphere.

Answer:

1. (1). For negative magnification object is placed beyond the focus:

⇒ \(m=\frac{v}{u}\)

using sign convention

∴ \(\mathrm{m}=-\frac{\mathrm{v}}{\mathrm{u}}\)

(2). For positive magnification object is placed between the focus and the optical centre.

⇒ \(m=\frac{v}{u}\)

Using sign convention \(\mathrm{m}=\frac{-\mathrm{v}}{-\mathrm{u}}\)

∴ \(m=\frac{v}{u}\)

Refraction through spherical surface ABC

⇒ \(\frac{\mathrm{n}_2}{\mathrm{v}^{\prime}}-\frac{\mathrm{n}_1}{\mathrm{u}}=\frac{\mathrm{n}_2-\mathrm{n}_1}{\mathrm{R}} \quad\left\{\begin{array}{l}
\text { Refractive index of glass }=3 / 2 \\
\mathrm{u}=-3 \mathrm{r}
\end{array}\right.\)

⇒ \(\frac{\frac{3}{2}}{v^{\prime}}-\frac{1}{\left(-3 r\right)}=\frac{\left(\frac{3}{2}-1\right)}{r} = \frac{3}{2 v^{\prime}}=\frac{1}{2 r}-\frac{1}{3 r} = v^{\prime}=9 r\)

Refractive through spherical surface ADC

For refracting surface ADC, the image I’ acts as a virtual object and 1 is the final image

⇒ \(\frac{\mathrm{n}_2}{\mathrm{v}}-\frac{\mathrm{n}_1}{\mathrm{u}^{\prime}}=\frac{\mathrm{n}_2-\mathrm{n}_1}{\mathrm{R}} = \frac{1}{\mathrm{v}}-\frac{1.5}{\mathrm{u}^{\prime}}=\frac{1-1.5}{-\mathrm{r}}\) (u’ = 9r – 2r = 7r)

∴ \(\frac{1}{v}-\frac{1.5}{7 r}=\frac{0.5}{r} = \frac{1}{v}=\frac{1}{2 r}+\frac{1.5}{7 r} = \frac{1}{v}=\frac{1.5}{7 r}+\frac{0.5}{r}=\frac{1.5+3.5}{7 r} = v =\frac{7 r}{5}\)

Distance of final image from ‘B’

∴ \(\frac{7 r}{5}+2 r=\frac{17 r}{5}=3.4 \mathrm{r}\)

 CBSE Class 12 Physics Chapter 9 Long Questions And Answers

Question 1. Optical fibres Nowadays optical fibres are extensively used for transmitting audio and video signals through long distances. Optical fibres too make use of the phenomenon of total internal reflection. Optical fibre arc fabricated with high-quality composite glass or quartz fibres.

Each fibre consists of a core and cladding. The refractive index of the material of the core is higher than that of the cladding. When a signal in the form of light is directed at one end of the fibre at a suitable angle, it undergoes repeated total internal reflections along the length of the fibre and finally comes out at the other end.

Since light undergoes total internal reflection at each stage, there is no appreciable loss in the intensity of the light signal. Optical fibres are fabricated such that light reflected at one side of the inner surface strikes the other at an angle larger than the critical angle.

Even if the fibre is bent, light can easily travel along its length. Thus, an optical fibre can be used to act as an optical pipe.

(1). Which of the following statements is not true?

1. Optical fibre is based on the principle of total internal reflection.
2. The refractive index of the material of the core is less than that of the cladding.
3. An optical fibre can be used to act as an optical pipe.
4. There is no appreciable loss in the intensity of the light signal while propagating through optical fibre.

Answer: 2. The refractive index of the material of the core is less than that of the cladding.

(2). What is the condition for total internal reflection to occur?

1. The angle of incidence must be equal to the critical angle.
2. The angle of incidence must be less than the critical angle.
3. The angle of incidence must be greater than the critical angle.
4. None of the above

Answer: 3. Angle of incidence must be greater than the critical angle.

(3). Which of the following is not an application of total internal reflection?

1. Mirage
2. Sparkling of diamond
3. Splitting of white light through a prism.
4. Reflects the prism.

Answer: 3. Splitting of white light through a prism.

(4). Optical fibres are used extensively to transmit:

1. Optical signal
2. Current
3. Sound waves
4. None of the above

Answer: 1. Optical signal

Question 2. The total internal reflection of the light is used in polishing diamonds to create a sparking brilliance. By polishing the diamond with specific cuts, it adjusted most of the light rays approaching the surface arc incident with an angle of incidence more than the critical angle. Hence, they suffer multiple reflections and ultimately come out of the diamond from the top. This gives the diamond a sparking brilliance.

(1). The refractive index for a diamond is

1. 1.41
2. Same as glass
3. 2.42
4. 1

Answer: 3. 2.42

(2). The basic reason for the extraordinary sparkle of a suitably cut diamond is that

1. It has a low refractive index
2. It has high transparency
3. It has a high refractive index
4. It is very hard

Answer: 3. It has a high refractive index

(3). The extraordinary sparkling of diamond

1. Docs do not depend on their shape
2. Depends on its shape
3. Has no fixed reason
4. None

Answer: 4. None

(4). Optical fibre cables work on the principle of

1. Dispersion of light
2. Refraction of light
3. Total internal reflection
4. Interference of light

Answer: 3. Total internal reflection

Question 3. A compound microscope consists of two converging lenses. One of them, of a smaller aperture and smaller focal length is called an objective and the other of a slightly larger aperture and slightly larger focal length is called an eye-piece. Both lenses are fitted in a tube with an arrangement to vary the distance between them. A tiny object is placed in front of the objective at a distance slightly greater than its focal length. The objective produces the image of the object which acts as an object for the eye-piece. The eyepiece, in turn, produces the final magnified image.

(1). In a compound microscope the images formed by the objective and the eye-piece are respectively.

1. Virtual, real
2. Real, virtual
3. Virtual, virtual
4. Real, real

Answer: 2. Real, virtual

(2). The magnification due to a compound microscope does not depend upon:

1. The aperture of the objective and the eye-piece
2. The focal length of the objective and the eye-piece
3. The length of the tube
4. The colour of the light used

Answer: 1. The aperture of the objective and the eye-piece

(3). Which of the following is not correct in the context of a compound microscope?

1. Both the lenses are of short Focal lengths.
2. The magnifying power increases by decreasing the local lengths of the two lenses.
3. The distance between the two lenses is more than (f₀ + f_c)
4. The microscope can be used as a telescope interchanging the two lenses.

Answer: 4. The microscope can be used as a telescope interchanging the two lenses

(4). A compound microscope consists of an objective of 10X and an eye-piece of 20X. the magnification due to the microscope would he:

1. 2
2. 10
3. 30
4. 200

Answer: 4. 200

(5). The focal length of the objective and eye-pic of a compound microscope arc is 1.2 cm and 3.0 cm respectively. The object is placed at a distance of 1.25 cm from the objective. If the final image is formed at infinity, the magnifying power of the microscope would be:

1. 100
2. 150
3. 200
4. 250

Answer: 3. 200

Question 4.

1. Plot a graph to show the variation of the angle of deviation as a function of the angle of incidence for light passing through a prism. Derive an expression for the refractive index of the prism in terms of the angle of minimum deviation and the angle of the prism.
2. What is the dispersion of light? What is its cause?
3. A ray of light incident normally on one face of a right-angled isosceles prism is reflected as shown. What must be the minimum value of the refractive index of glass? Give relevant calculations.

Answer:

Let PQ and RS be incident and emergent rays. Let the incident ray get deviated by (δ) in a prism.

i.e. ∠TMS = δ

δ₁ and δ₂ are deviations produced at surfaces AB and AC respectively.

∴ δ = δ₁ + δ₂

δ = ( i₁ – r₁ ) + ( i₂ – r₂ )

δ = ( i₁ +i₂ )- ( r₁ +r₂ ) → (1)

In quadrilateral AQNR,

A + ∠QNR = 180° ( ∵ QN, RN are normal)

Also, in ΔQNR, ∠QNR + r₁ + r₂ = 180°

δ = r₁ + r₂ → (2)

From eq (1) and (2), we get

δ = ( i₁ +i₂ )- A →(3)

The angle of deviation produced by the prism varies with the angle of incidence. When the prism is adjusted at an angle of minimum deviation, then

i₁ = i₂ = i (suppose)

at δ = δ_m

⇒ r₁ = r₂ = r (suppose)

From (1) and (2) we have,

δ_m = 2i – 2r

and 2r = A

⇒ \(i=\frac{A+\delta_{m}}{2}\)

r = A/2

∴ Refractive index of material of prism is \(\mu=\frac{\sin \mathrm{i}}{\sin \mathrm{r}}=\frac{\sin \left(\frac{\mathrm{A}+\delta_{\mathrm{m}}}{2}\right)}{\sin \left(\frac{\mathrm{A}}{2}\right)}\).

2. The splitting of white light into bands of seven different colours (V, I, B, g, Y, O, R) is called dispersion of white light.

Cause: Different colours travel with velocity while passing through a prism so they get separated.

From geometry, the angle of incidence at the surface (AC) is 45°. Now as shown ray MN gets reflected at angle 45, i.e, i > i_c

From \(\mu=\frac{1}{\sin i_c}=\frac{1}{\sin 45^{\circ}}=\sqrt{2}\)

Question 5.

1. Draw a ray diagram to show the image formation by a combination of two thin convex lenses in contact. Obtain the expression for the power of this combination in terms of the focal lengths of the lenses.
2. A ray of light passing from the air through an equilateral glass prism undergoes minimum deviation when the angle of incidence is \(\left(\frac{3}{4}\right)^{\mathrm{th}}\) of the angle of prism. Calculate the speed of light in the prism.

Answer:

The object is placed at point O. whose image is formed at me, by the first lens. As image I₁ is real, it works as a virtual object for second lens B, producing the final image at I.

Since the lenses are thin, assume the optical centres to be coincident. Let this central point be p.

For the image formed by lens A.

\(\frac{1}{v_1}-\frac{1}{u}=\frac{1}{f_1}\) → (1)

Similarly, for the lens B,

\(\frac{1}{v}-\frac{1}{v_1}=\frac{1}{f_2}\) → (2)

Add (1) and (2) we get,

If a lens system is taken as equivalent to a single lens of focal length f, we get.

\(P=\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\) → (3)

In terms of power, equation (3) can be written as,

P = P₁ + P₂

Where P is the net power of this combination.

2. Given: (A = angle of prism)

• ABC is an equilateral triangle. [A = 60°]
• \(\angle \mathrm{i}=\frac{3}{4} \mathrm{~A}\)

we know that,

δ =i + c- A

Now in the condition of min. deviation,

i = e, therefore we can write,

δ_m = i +i- A

or \(\delta_{\mathrm{m}}=2 \mathrm{i}-\mathrm{A} \text { or } \delta_{\mathrm{m}}=2\left(\frac{3 \mathrm{~A}}{4}\right)-\mathrm{A}\)

⇒ \(\delta_{\mathrm{m}}=\frac{3 \mathrm{~A}}{2}-\mathrm{A}=\frac{\mathrm{A}}{2}=30^{\circ}\)

⇒ δ_m = 30°

Now, \(\mu=\frac{\sin \left(\frac{A+\delta_m}{2}\right)}{\sin \left(\frac{A}{2}\right)}=\frac{\sin \left(\frac{60^{\circ}+30^{\circ}}{2}\right)}{\sin \left(\frac{60^{\circ}}{2}\right)}\)

⇒ \(\mu=\frac{\sin 45^{\circ}}{\sin 30^{\circ}}=\sqrt{2}\)

So, \(v=\frac{c}{\mu}=\frac{3 \times 10^8}{\sqrt{2}}=2.1 \times 10^8 \mathrm{~m} / \mathrm{s}\)

Question 6. A point object O on the principal axis of a spherical surface of radius of curvature R separating two media of refractive indices ni and m forms an image T.

Prove that: \(\frac{n_2}{v}-\frac{n_1}{u}=\frac{n_2-n_1}{R}\)

Answer:

Assumptions:

• The Aperature of the spherical refracting surface is small.
• The object is a point object and lies on the principal axis.
• Incident ray, refracted ray and normal to the spherical surface make small angles with PA.

Let, XPY = Convex spherical refracting surface.

0 = Point object in rarer medium

I = Real image in a denser medium

From ΔAOC, i = α + γ

From ΔAIC, γ = r + β ⇒ r = γ – β

From snell’s law, \(\frac{\sin i}{\sin r}=\frac{n_2}{n_1} ⇒ n_1 \sin i=n_2 \sin r\)

Since the angles are small,

∴ n₁ i = n₂ r

Substituting for i and r, in the above eqn, we get

⇒ n₁ (α + γ) = n₂ (γ – β)

or \(n_1\left\{\frac{\mathrm{AM}}{\mathrm{PO}}+\frac{\mathrm{AM}}{\mathrm{MC}}\right\}=\mathrm{n}_2\left\{\frac{\mathrm{AM}}{\mathrm{MC}}-\frac{\mathrm{AM}}{\mathrm{MI}}\right\}\)

Since the aperature is small,

∴ MC = PC, MI = PI

∴ \(\left\{\frac{n_1}{P O}+\frac{n_1}{P C}\right\}=\left\{\frac{n_2}{P C}-\frac{n_2}{P l}\right\}\)

Acc. to sign convention,

PO = -u. PC = R, PI = v

∴ \(\left\{\frac{n_1}{-u}+\frac{n_1}{R}\right\}=\left\{\frac{n_2}{R}-\frac{n_2}{v}\right\}\)

or. \(\frac{n_2}{v}-\frac{n_1}{u}=\frac{n_2-n_1}{R}\)

Question 7.

1. Derive lens maker’s formula. Draw the necessary diagram.
2. A convex lens is placed over a plane mirror. A pin is now positioned so that there is no parallax between the pin and its image formed by this lens-mirror combination. How will you use this observation to find the focal length of the lens? Explain briefly.

Answer:

1. Lens maker’s formula

∴ \(\frac{1}{f}=(n-1)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)

Assumptions:

1. The lens is considered a thin lens.
2. An object is a point object which is situated on the principal axis.
3. The aperture of the lens is small.
4. Incident and refracted rays make a small angle with the principal axis.

Consider a thin convex lens of absolute refractive index n₂ placed in a rarer medium of absolute refractive index n₁. Also, R₁ and R₂ are the radii of curvature of surfaces XP₁ Y and XP₂ Y respectively.

For refraction at surface XP₁ Y:

‘O’ is the object and I’ is its real image.

Using formula,

⇒ \(\frac{n_2}{v}-\frac{n_1}{u}=\frac{n_2-n_1}{R}\) we get,

⇒ \(\frac{n_2}{v^{\prime}}-\frac{n_1}{u}=\frac{n_2-n_1}{R_1}\) → (1)

For refraction at surface XP₂ Y:

F is the virtual object &I is its real image (final image).

Using formula

⇒ \(\frac{n_1}{v}-\frac{n_2}{u}=\frac{n_1-n_2}{R}\)

⇒ \(\frac{n_1}{v}-\frac{n_2}{v^{\prime}}=\frac{n_1-n_2}{R_2}\) → (2)

Adding equations (1) and (2). we get

⇒ \(n_1\left(\frac{1}{v}-\frac{1}{u}\right)=\left(n_2-n_1\right)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)

⇒ \(\frac{1}{v}-\frac{1}{u}=\frac{n_2-n_1}{n_1}\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)

or \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}=\left(\frac{n_2}{n_1}-1\right)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)

or \(\frac{1}{f}=(n-1)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\) (\(\frac{n_2}{n_1}=n_1=n\))

2. The rays must fall normally on the plane mirror so that the image of the pin coincides with itself.

∴ P is the position of the locus of the lens. i.e.

Distance OP = focal length

CBSE Class 12 Physics Chapter 12  Atom Multiple Choice Questions And Answers

Question 1. The radius of the second orbit in a hydrogen atom is R. What is the radius in the third orbit?

1. 3R
2. 2.25 R
3. 9R
4. R/3

Answer: 2. 2.25 R

Read and Learn More Important Questions for Class 12 Physics with Answers

W.k.t Radius is n^th orbit

rn = n²R’ → (1)

R = 4R’ → (2) [For 2 Orbit, n= 2]

r₃ = 9R’ → (3) [For 2 Orbit, n= 3]

= \(9 \times \frac{R}{4}\)

∴ r₃ = 2.25 R

Question 2. The wavelength of the first line of the Lyman series is X. The wavelength of the first line in the Balmer series is ______.

1. \(\frac{27}{5} \lambda\)
2. \(\frac{5}{27} \lambda\)
3. \(\frac{9}{2} \lambda\)
4. \(\frac{2}{5} \lambda\)

Answer: 1. \(\frac{27}{5} \lambda\)

⇒ \(\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

⇒ \(\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{1}-\frac{1}{2^2}\right)=\frac{3}{4} \mathrm{R} \Rightarrow \mathrm{R}=\frac{4}{3} \lambda\)

So, for Balmer series (n₁ = 2, n₂ = 3)

⇒ \(\frac{1}{\lambda^{\prime}}=\mathrm{R}\left(\frac{1}{4}-\frac{1}{9}\right)\)

⇒ \(\frac{1}{\lambda^{\prime}}=\frac{4}{3 \lambda}\left(\frac{5}{36}\right)\)

∴ \(\lambda^{\prime}=\frac{27 \lambda}{5}\)

Question 3. For the first orbit of hydrogen atom the minimum excitation potential is ______ V.

1. 13.6
2. 3.4
3. 10.2
4. 3.6

Answer: 3. 10.2

Question 4. An electron with an energy of 12.09 eV strikes a hydrogen atom In the ground state and gives its all energy to the hydrogen atom. Therefore hydrogen atoms are excited to _______ stale.

1. Fourth
2. third
3. Second
4. First

Answer: 3. Second

⇒ \(E_n=-\frac{13.6}{n^2}\)

Toral energy gained by hydrogen atoms is

-13.6+12.09 =-1.51 eV

So, \(n^2=\frac{-13.6}{-1.51}=9 \Rightarrow n=3\)

So, second excited state.

Question 5. The ratio of energies of electrons in a second excited state to the first excited slate in H-atom:

1. 1:4
2. 9:4
3. 4:9
4. 4:4

Answer: 3. 4:9

⇒ \(E_n=-13.6 \frac{z^2}{n^2}\) (used it)

For the second excited state n = 3 and the first excited state n = 2

∴ \(\frac{E_2}{E_1}=\frac{4}{9}\)

Question 6. For the first orbit of the hydrogen atom, the minimum excitation potential is ______V.

1. 13.6
2. 3.4
3. 10.2
4. 3.6

Answer: 3. 10.2

Question 7. If the potential energy of the electron in the hydrogen atom is \(\frac{-e^2}{4 \pi \varepsilon_0 r}\), then what is its kinetic energy?

1. \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\)
2. \(\frac{-e^2}{4 \pi \varepsilon_0 r}\)
3. \(\frac{-e^2}{8 \pi \varepsilon_0 r}\)
4. \(\frac{e^2}{4 \pi \varepsilon_0 r}\)

Answer: 1. \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\)

⇒ \(k_n=-\frac{U n}{2}\)

∴ \(k_n=+\frac{e^2}{8 \pi \varepsilon_0 r}\)

Question 8. What is the angular momentum of an electron of Li-alom in n = 5 orbit?

1. 6.625 x 10^-34 Js
2. 5.27 x 10^-34 Js
3. 1.325 x 10^-34 Js
4. 16.56 x 10^-34 Js

Answer: 2. 5.27 x 10^-34 Js

⇒ \(\mathrm{mvr}=\frac{\mathrm{nh}}{2 \pi}\)

⇒ \(\frac{5 \times 6.62 \times 10^{34}}{2 \times 3.14}\)

∴ 5.27 x 10^-34 Js

Question 9. A hydrogen atom absorbs 12.1 eV of energy and gets excited to a higher energy level. How many photons are emitted during the downward transition? Assume during each downward transition, one photon is emitted.

1. 2 or 3
2. 1 or 3
3. 1 or 2
4. 5 or more

Answer: 3. 1 or 2

Question 10. 13.6 eV energy is required to separate a hydrogen atom into a proton and an electron. Compute the orbital radius of the corresponding electron.

1. 5.3 x 10^-11 m
2. 10.6 x 10^-11 m
3. 2.65 x 10^-11 m
4. 1.33 x 10^-11 m

Answer: 1. 5.3 x 10^-11 m

⇒ \(\mathrm{E}=-\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\)

⇒ \(r=-\frac{e^2}{8 \pi \varepsilon_0 E}\)

By solving r = 5.29 x 10^-11 m

or

⇒ \(r_1=0.529 \frac{n^2}{Z} Å\)

∴  0.529 A

Question 11. What is the shortest wavelength present in the Paschcn scries of spectral lines?

1. 821 nm
2. 6563 A
3. 911 nm
4. 656 mm

Answer: 1. 821 nm

⇒ \(\frac{1}{\lambda}=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

⇒ \(\frac{1}{\lambda}=1.097 \times 10^7\left(\frac{1}{9}-\frac{1}{\infty}\right)\)

λ = 8.21 x 10^-7 m

λ = 821 x nm

Question 12. The total energy and kinetic energy of an electron in hydrogen atom arc E and K respectively.

1. K = 2 E
2. K = -E
3. \(K=\frac{E}{2}\)
4. K = E

Answer: 2. K = -E

Question 13. The ionization energy of an electron in the third excited state for a hydrogen atom is _______ eV.

1. 13.6
2. 1.51
3. 0.85
4. 3.4

Answer: 3. 0.85

⇒ \(E_n=-\frac{13.6}{n^2}\)

energy of the third excited state

⇒ \(-\frac{13.6}{16}=-0.8 .5 \mathrm{eV}\)

So Ionisation energy

= + 0.85 eV

Question 14. In the Geiger-Marsden scattering experiment, thin gold foil is used to scatter alpha particles because alpha particles will

1. Not suffer more than one scattering and the gold nucleus is 50 times heavier than the alpha particle.
2. Not suffer more than one scattering and the gold nucleus is lighter than the alpha particle.
3. Not suffer more than a few scattering and the gold nucleus is 25 times heavier than the alpha particle.
4. Suffer more than one scattering and the gold nucleus is 25 times heavier than an alpha particle.

Answer: 1. Not suffer more than one scattering; the gold nucleus is 50 times heavier than the alpha particle.

Atoms Assertion And Reason

For question numbers 1 to 5 two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (1), (2), (3), and (4) as given below.

1. Both A and R are true and R is the correct explanation of A
2. Both A and R are true but R is NOT the correct explanation of A
3. A is true but R is false
4. A is false and R is also false

Question 1. Assertion: The mass of the atom is concentrated in the nucleus.

Reason: The mass of a nucleus can be either less than or more than the sum of the masses of nucleons present in it.

Answer: 3. A is true but R is false

Question 2. Assertion: Bohr’s orbits are also called stationary stales.

Reason: In Bohr’s orbits electron revolves in a fixed path.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 3. Assertion: A hydrogen atom consists of only one electron but its emission spectrum has many lines.

Reason: The Lyman series is found in the emission spectrum.

Answer: 2. Both A and R are true but R is NOT the correct explanation of A

Question 4. Assertion: For the scattering of a-particles at a large angle only the nucleus of the atom is responsible.

Reason: Nucleus is very heavy in comparison to electrons.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 5. Assertion: Atom arc is not electrically neutral.

Reason: The number of protons and electrons is different

Answer: 4. A is false and R is also false

CBSE Class 12 Physics Chapter 12  Atoms Short Questions And Answers

Question 1. Show that the radius of the orbit in a hydrogen atom varies as n² where n is the principal quantum number of the atom.

Answer:

Coulomb force: The electrostatic attraction force between the electron and nucleus is _______

⇒ \(\mathrm{F}_{\mathrm{e}}=\frac{\mathrm{kZe}^2}{\mathrm{r}_{\mathrm{n}}^2}\) → (1) \(\left\{\mathrm{F}_{\mathrm{e}}=\frac{\mathrm{k} \mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2}\right.\)

Centripetal Force = \(\frac{m v_n^2}{r_n}\)

In equilibrium \(\frac{m v_n^2}{r_n}=\frac{k Z e^2}{r_n^2}\)

⇒ \(\mathrm{v}_{\mathrm{n}}^2=\frac{\mathrm{kZe^{2 }}}{\mathrm{mr}_{\mathrm{n}}}\) → (2)

Then form Bohr’s second postulate \(m v_n r_n=\frac{n h}{2 \pi}\)

∴ \(\mathrm{v}_{\mathrm{n}}=\frac{\mathrm{nh}}{2 \pi \mathrm{mr}_{\mathrm{n}}}\) → (3)

From eq (2) and (3)

⇒ \(\frac{n^2 h^2}{4 \pi^2 m^2 r_n^2}=\frac{k Z e^2}{m r_n}\)

⇒ \(r_n=\left(\frac{h^2}{4 \pi^2 e^2 k m}\right) \frac{n^2}{Z}\)

Put the value, π, k, h, m, e

∴ \(r_n=0.529 \times 10^{-8} \times \frac{n^2}{Z} \mathrm{~cm}=0.529 \times \frac{n^2}{Z}Å\)

Question 2. How does one explain, Bohr’s second postulate of quantization of orbital angular momentum using the de Broglie’s hypothesis?

Answer:

The behavior of particle waves can be viewed as analogous to the waves traveling on a siring. Particle waves can lead to standing waves held under resonant conditions. When a stationary string is plucked, several wavelengths are excited but only those wavelengths survive which form a standing wave in the string.

Thus, in a string standing waves arc formed only when the total distance traveled by f a wave is an integral number of wavelengths. Hence, for any electron moving in a circular orbit of radius r_n, the total distance is equal to the circumference of the orbit. 2πr_n .

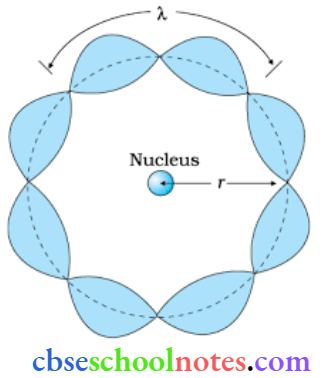
2πr_n = n → (1)

Here, λ is de Broglie wavelength.

We know

λ = h/p

or λ = h/mv_n → (2)

Where mv_n is the momentum of an electron revolving in the nth orbit,

From equation (2) and equation (1) we get.

2πr_n = nh/mv_n

L = mv_n r_n = nh/2π

Hence, de Broglie’s hypothesis successfully proves Bohr’s second postulate.

Question 3. Given the value of the ground state energy of hydrogen atom as -13.6 eV, find out its kinetic and potential energy in the ground and second excited states.

Answer:

Ground stale energy of hydrogen atom as -13.6 eV,

E_n = Total energy = \(-\frac{13.6 \mathrm{eV}}{n^2}\)

K.e = -T.E and P.e = 2 T.E

For ground stale n = 1, then

⇒ \(\mathrm{T} . \mathrm{E} .=\frac{-13.6 \mathrm{eV}}{(1)^2}=-13.6 \mathrm{eV}\)

K.E. = +13.6 eV

P.E. = -27.2 eV

For second excited state n = 3, then

∴ \(\text { T.E. }=\frac{-13.6}{9}=-1.51 \mathrm{eV}\)

K.E. = +1.51 eV

P.E. = -3.02 eV

Question 4. Given the ground stale energy E₀ = -13.6 cV and Bohr radius r₀ = 0.53 Å. Find out how the dc Broglie wavelength associated with the electron orbiting in the ground stale would change when it jumps into the first excited state.

Answer:

Given ground slate energy E₀ = – 13.6 eV

Energy in the first excited state = \(E_1=\frac{-13.6 \mathrm{eV}}{(2)^2}=-3.4 \mathrm{eV}\)

∴ \(\lambda=\frac{h}{\sqrt{2 \mathrm{mE}_1}}=\frac{6.63 \times 10^{-34}}{\sqrt{2 \times\left(9.1 \times 10^{-31}\right)\left(3.4 \times 1.6 \times 10^{-19}\right)}}\)

∴ \(\lambda=\frac{6.63 \times 10^{-34}}{9.95 \times 10^{25}}=6.66 \times 10^{-10} \mathrm{~m} \simeq 6.7 \times 10^{-10} \mathrm{~m}\)

Question 5. A hydrogen atom initially in the ground slate absorbs a photon with energy 12.5 eV. Calculate the longest wavelength of the radiation emitted and identify the series to which it belongs.

Answer:

We Know, \(\frac{1}{\lambda_{\max }}=R\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)\)

The energy of the incident photon = 12.5 eV

Energy of ground stale = -13.6 eV

∴ The energy of the hydrogen atom after absorption of a photon can be -1.1 eV

This means that electrons can go to the excited state n_i = 3. Now it emits photons of maximum wavelength on going to n_f = 2

⇒ \(\frac{1}{\lambda_{\max }}=\mathrm{R}\left\{\frac{1}{2^2}-\frac{1}{3^2}\right\}\)

⇒ \(\lambda_{\text {mat }}=\frac{36}{5 \mathrm{R}}=\frac{36}{5 \times 1.1 \times 10^7}=6.545 \times 10^{-7} \mathrm{~m}=6.545 \mathrm{~A}^{\circ}\)

It belongs to the Balmer Series.

Question 6. When is the H_α line in the emission spectrum of the hydrogen atom for the Balmer series obtained? Calculate the frequency of the photon emitted during this transition.

Answer: 

H_α is a specific deep-red visible spectral line in the Balmer series with a wavelength of 656.28 nm, it occurs when a hydrogen electron transits from its 3^rd to 2^nd lowest energy level.

This transition produces an H-alpha photon and the 1^st line of the Balmer series.

⇒ \(\frac{1}{\lambda}=R\left[\frac{1}{n_f^2}-\frac{1}{n_i^2}\right]\)

⇒  \(\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{3^2}\right] \Rightarrow \frac{1}{\lambda}=1.097 \times 10^7\left[\frac{5}{36}\right]\)

∴ \(v=\frac{c}{\lambda}=\frac{3 \times 10^8 \times 1.097 \times 10^7 \times 5}{36}\) = 4.57 x 10¹⁴ Hz

Question 7. The energy levels of a hypothetical atom are shown below. Which of the shown transitions will result in the emission of a photon of wavelength 275 nm?

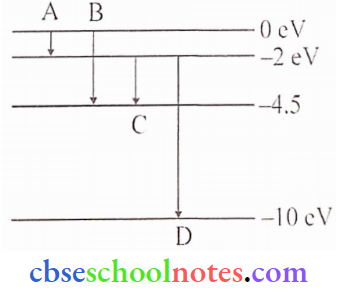
Answer:

Using relation, \(\mathrm{E}=\frac{1242 \mathrm{eV}}{\lambda(\text { in } \mathrm{nm})}\)

Here, = 275nm, \(\mathrm{E}=\frac{1242}{275}=4.5 \mathrm{eV}\)

This energy of photon exists corresponding to ‘B’.

Question 8. State Bohr’s postulate of hydrogen atom which successfully explains the emission lines in the spectrum of hydrogen atom.

Use the Rydberg formula to determine the wavelength of the line.

[Given : Rydberg constant R = 1.03 x 10⁷ m^-1]

Answer:

According to Bohr’s postulate when an e^– jumps from one orbit to another, the energy difference between them is emitted in the form of energy i.e. as a photon which shows the emission lines in the spectrum of hydrogen atoms.

⇒ \(E_i-E_f=h \nu=\frac{h c}{\lambda}\)

Now, the Rydberg formula for the Balmer series is

⇒ \(\frac{1}{\lambda}=R\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)\) where R = Rydberg constant = 1 .09 x 10⁷ m^-1

The H_α– line of the Balmer series is obtained when an e jumps to the second orbit (nf = 2) from
the third orbit (n. = 3).

Further, \(\frac{1}{\lambda}=1.03 \times 10^7\left(\frac{1}{2^2}-\frac{1}{3^2}\right)=6.99 \times 10^{-7}=699 \mathrm{~nm}\)

‘λ’ lies in the visible region.

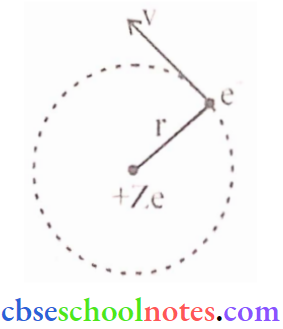
Question 9. Using Rutherford’s model of the atom, derive the expression for the total energy of a tin electron in the hydrogen atom. What is the significance of total negative energy possessed by the electron?

Answer:

According to Rutherford’s nuclear model of the atom, the electrostatic force of attraction F_e between the revolving electron and the nucleus provides the centripetal force (F_c).

Thus, F_c = F_e

∴ \(\frac{m v^2}{r}=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{e^2}{r^2}\) (∵ z = 1)

Thus the relation between the orbit radius and the e- velocity is, \(\mathrm{r}=\frac{\mathrm{e}^2}{4 \pi \varepsilon_0 \mathrm{mv}^2}\)

The K.E. (K) and electrostatic potential energy (U) of electrons in hydrogen atoms are

⇒ \(K=\frac{1}{2} m v^2=\frac{e^2}{8 \pi \varepsilon_0 r}\)

and \(\mathrm{U}=\frac{-\mathrm{e}^2}{4 \pi \varepsilon_0 \mathrm{r}}\) (-ve sign shows, that the nature of force is attractive)

Thus, the total rnech. energy E of an e^– is,

∴ \(\mathrm{E}=\mathrm{K}+\mathrm{U}=\frac{\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}-\frac{\mathrm{e}^2}{4 \pi \varepsilon_0 \mathrm{r}}=\frac{-\mathrm{e}^2}{8 \pi \varepsilon_0 \mathrm{r}}\)

Total energy (E) is -ve which shows that e^– is bound to the nucleus, if (E) were +ve then e- would leave the the atom.

Question 10.

1. Stale Bohr’s postulate of the hydrogen atom gives the relationship to the frequency of emitted photons in a transition.
2. An electron jumps from the fourth to the first orbit in an atom. How many maximum number of spectral lines can be emitted by the atom? To which series do these lines correspond?

Answer:

1. According to Bohr’s theory, energy is quantized i.c. for each orbital the corresponding energy is
given as

ΔE = hv

2. There will be 6 spectral lines and they correspond to.

Max. number of spectral lines = \(\frac{n(n-1)}{2}\)

For the fourth orbit n = 4

Then, Max. possible lines = \(\frac{4(4-1)}{2}\)

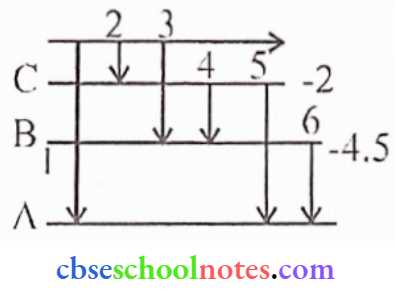
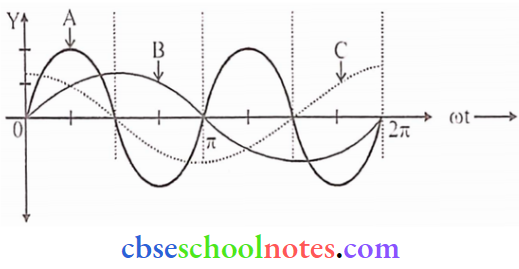
A-Lyman Series, B-Balmcr series, C-Paschcn series

Question 11. A 12.5 eV electron beam is used to excite a gaseous hydrogen atom at room temperature. Determine the wavelengths and the corresponding series of the lines emitted.

Answer:

When an electron beam of 12.5 eV is used to excite hydrogen, then the probable transition is from n=1 to n=3 (i.e. E₃-E₁ = -1.5l-(-l 3.6) = 12.09e V)

On de-excitation, the electron may jump by following the ways

3 → I, 3 → 2, 2 → 1

Possible wavelength and their corresponding series of lines emitted are

1. From n=3 to n = 1, \(\frac{1}{\lambda}=R\left[\frac{1}{1^2}-\frac{1}{3^2}\right] \Rightarrow \frac{1}{\lambda}=R\left[1-\frac{1}{9}\right]=R\left(\frac{8}{9}\right)\)

or \(\lambda=\frac{9}{8 \mathrm{R}}=1.026 \times 10^{-7} \mathrm{~m}=102.6 \mathrm{~nm}\)

It belongs to the Lyman series.

2. From n = 3 to n = 2,

⇒ \(\frac{1}{\lambda}=R\left[\frac{1}{2^2}-\frac{1}{3^2}\right]=R\left[\frac{1}{4}-\frac{1}{9}\right] \Rightarrow \frac{1}{\lambda}=R\left[\frac{5}{36}\right]\)

∴ \(\lambda=\frac{36}{5 \mathrm{R}}=6.563 \times 10^{-7} \mathrm{~m}=656.3 \mathrm{~nm}\)

It belongs to the Balmer series.

3. From n = 2 to n = 1,

⇒ \(\frac{1}{\lambda}=R\left[\frac{1}{1^2}-\frac{1}{2^2}\right]=R\left[1-\frac{1}{4}\right] \Rightarrow \frac{1}{\lambda}=\frac{3 R}{4}\)

A = 1.215 x 1 0^-7m = 121.5 nm

It belongs to the Lyman series.

Question 12.

1. In A Geiger-Marsden Experiment. Find the distance of the closest approach to the gold nucleus (mass no. = 79)m of a 7.7 Me V α-particle before it comes momentarily to rest and reverses its direction.
2. Plot a graph between several scattered α-particles detected in the gold foil experiment and the angle of scattering. What is the main assumption in plotting this graph?

Answer:

K.E. = P.E

⇒ \(K E_{\alpha}=\frac{k q_1 q_2}{r}\) where q₁ = 79e, q₂ = 2e

So r = \(\mathrm{r}=\frac{\mathrm{kq}_1 \mathrm{q}_2}{\mathrm{KE}_\alpha}=\frac{9 \times 10^9 \times\left(79 \times 1.6 \times 10^{-19}\right)\left(2 \times 1.6 \times 10^{-19}\right)}{7.7 \times 10^6 \times 1.6 \times 10^{-19}}=\frac{18 \times 79 \times 1.6}{7.7} \times 10^{-16} \mathrm{~m}\)

r = 295.4 x 10^-16 = 29.54 m = 30 fm

0 = Scattering angle

N= No. of α-Particles

The plot is Schematic and not according to scale.

Question 13.

1. state Bohr’s quantization condition for defining stationary orbits. How does de Broglie’s hypothesis explain the stationary orbits?
2. Find the relation between the three wavelengths λ_1, λ₂, λ₃ and from the energy level diagram shown below.

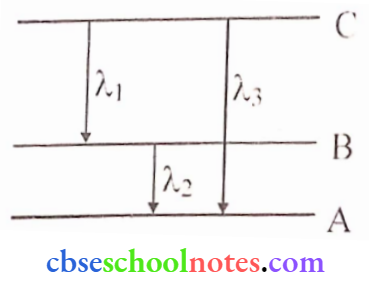
Answer:

1. Bohr’s quantization condition: The electron can revolve around the nucleus only in those circular orbits in which the angular momentum of an electron is an integral multiple of \(\frac{h}{2 \pi}\), where h is Planck’s constant. \(\mathrm{mvr}=n \frac{\mathrm{h}}{2 \pi}\) [m = mass, v = velocity of electron]

Their circular orbits are stationary, de Broglie hypothesis: de-Broglie interprets Bohr’s 2^nd postulate in terms of the wave nature of the electron. According to him- The electron can revolve in certain stable orbits for which the angular momentum is some integral multiple of h/2π.

Mathematically, \(2 \pi r_n=\frac{n h}{m v}\)

Therefore, \(\mathrm{mvr}_{\mathrm{n}}=\frac{\mathrm{nh}}{2 \pi}\)

2. \(E_{C B}=\frac{h c}{\lambda_1} \Rightarrow E_{B A}=\frac{h c}{\lambda_2} \Rightarrow E_{C A}=\frac{h c}{\lambda_3}\)

here E_CB = Energy gap between levels B and C

E_CA = Energy gap between levels A and C

E_BA= Energy gap between levels A and B

E_CA = E_CB + E_BA

∴ \(\frac{h c}{\lambda_3}=\frac{h c}{\lambda_1}+\frac{h c}{\lambda_2} \Rightarrow \frac{1}{\lambda_3}=\frac{1}{\lambda_1}+\frac{1}{\lambda_2} \Rightarrow \lambda_3=\frac{\lambda_1 \lambda_2}{\lambda_1+\lambda_2}\)

Question 14. State Bohr’s postulate to explain stable orbits in a hydrogen atom. Prove that the speed with which the electron revolves in nlh orbit is proportional to (1/n).

Answer:

Bohr’s postulate:

Electron revolves around the nucleus in those orbits for which the angular momentum is an
integral multiple of h/2π.

∴ \(\mathrm{mvr}=\frac{\mathrm{nh}}{2 \pi}\)

Speed of e^– in n^th orbit

For hydrogen radius of nth orbit is given by = \(r_n=\frac{\varepsilon_0 n^2 h^2}{\pi m c^2}\)

Form Bohr’s postulate

⇒ \(m v_n r_n=\frac{n h}{2 \pi}\)

⇒ \(m v_n\left(\frac{\varepsilon_0 n^2 h^2}{\pi m e^2}\right)=\frac{n h}{2 \pi}\)

∴ \(\mathrm{V}_{\mathrm{n}}=\frac{\mathrm{c}^2}{2 \varepsilon_0 h n} \Rightarrow \mathrm{V}_{\mathrm{n}} \propto \frac{1}{\mathrm{n}}\)

Question 15. A narrow beam of protons, each having 4.1 MeV energy is approaching a sheet of lead (Z = 82). Calculate :

1. The speed of a proton in the beam, and
2. The distance of its closest approach

Answer:

Energy of proton = 4. 1 MeV, Z = 82

1. Speed of a proton

⇒ \(\frac{1}{2} m_p v_p^2=4.1 \times 10^6 \times 1.6 \times 10^{-19}\)

∴ \(v_p^2=\frac{2 \times 4.1 \times 1.6 \times 10^{-13}}{1.67 \times 10^{-27}}=7.85 \times 10^{14}\)

V_p = 2.8 x 10⁷ m/s

2. Distance of closest approach

⇒ \(K. E=\frac{k e(z e)}{r_0}\)

⇒\(r_0=\frac{K Z e^2}{r_0}=\frac{9 \times 10^{9} \times 82 \times\left(1.6 \times 10^{-19}\right)^2}{4.1 \times 10^6 \times 1.6 \times 10^{-19}}=288 \times 10^{-16}\)

∴r₀ = 2.9 x 10^-14 m^-1

CBSE Class 12 Physics Chapter 12  Long Questions And Answers

Question 1. According to the third postulate of Bohr’s model, when an atom makes a transition from the higher energy stale with quantum number nj to the lower energy stale with quantum number n_f(n_f <n_i), the difference of the energy is carried away by the photon of frequency such that hv = En_i-En_f.

Since both ni and nf are integers, this immediately shows that in transitions between the different atomic levels, light is radiated in various discrete frequencies. For the hydrogen atom spectrum, the Balmcr formula corresponds to n_f = 2 and n_i = 3, 4, 5, etc. This result of Bohr’s model suggested the presence of other scries spectra for hydrogen atoms – those corresponding to the transitions resulting from n_f = 1 and n_i = 2, 3, etc: and n_f = 3 and n_i = 4, 5, etc., and so on. Such series were identified in the course of spectroscopic investigations and are known as the Lyman, Balmer, Paschen, Brackett, and Pfund series. The electronic transitions corresponding to this series are shown

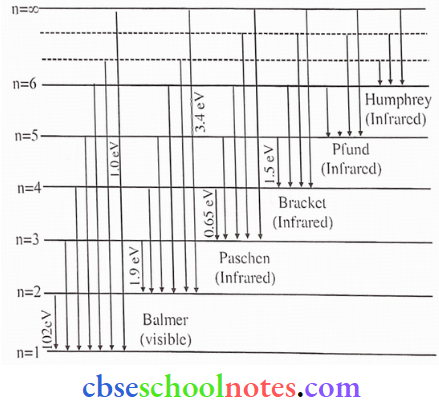
(1). The total energy of an electron in an atom in an orbit is -3.4 eV. Its kinetic and potential energies are respectively

1. 3.4 eV, 3.4 eV
2. -3.4 eV, -3.4 eV
3. -3.4eV,-6.8 eV
4. 3.4 eV, -6.8 eV

Answer: 4. 3.4 eV, -6.8 eV

(2). Given the value of the Rydberg constant is 10⁷ m^-1, the wave number of the last line of the Balmer series in the hydrogen spectrum will be

1. 0.5 x 10⁷ m^-1
2. 0.25 x 10⁷ m^-1
3. 2.5 x 10⁷ m^-1
4. 0.025 x 10⁴ m^-1

Answer: 2. 0.25 x 10⁷ m^-1

(3). The ratio of the wavelength of the last line of Balmcr scries and the last line of the Lyman series

1. 0.5
2. 2
3. 1
4. 4

Answer: 4. 1

(4). The wavelength of Balmer scries lies in

1. Ultraviolet region
2. Infrared region
3. Far infra-red region
4. Visible region

Answer: 4. Visible region

Question 2. Neutrons mid protons tire identical particles in the sense that their masses are nearly the same and the force called nuclear force, does not distinguish between them, Nuclear force is the strongest force. The stability of the nucleus is determined by the neutron Proton ratio or mass defect or packing fraction, The Shape of the nucleus is calculated by quadruple moment and the spin of the nucleus depends on an even or odd mass number. The volume of the nucleus depends on the mass number. The whole mass of the atom (nearly 99%) is centered at the nucleus.

(1). The correct statement about the nuclear force is as follows:

1. Charge independent
2. Short range force
3. Nonconservative force
4. All of these

Answer: 4. All of these

(2). The range of a nuclear force is the order of:

1. 2 x 10^-10 m
2. 1.5 x 10^-20 m
3. 1.2 x 10^-4m
4. 1.4 x 10^-15 m

Answer: 4. 1.4 x 10^-15 m

(4). A force between two protons is the same as the force between a proton and a neutron. The nature of the force is:

1. Electrical force
2. Weak nuclear force
3. Gravitational force
4. Strong nuclear force

Answer: 1. Electrical force

CBSE Class 12 Physics Chapter-3 Current Electricity Multiple Choice Questions And Answers

Question 1. In the circuit given below P≠R and the reading of the galvanometer is the same with switch S open or closed. Then:

1. I_Q=I_R
2. I_R=I_G
3. I_P=I_G
4. I_Q+I_G

Answer: 4. I_Q+I_G

Read and Learn More Important Questions for Class 12 Physics with Answers

Question 2. Two wires A and B of the same material having length in the ratio 1:2 and diameter in the ratio 2:3 are connected in series with a battery. The ratio of the potential differences (V_A/V_B) across the two wires respectively is:

1. 1/3
2. 3/4
3. 4/5
4. 9/8

Answer: 4. 9/8

In Series, I → Same.

V = IR

⇒ \(\frac{V_A}{V_B}=\frac{R_A}{R_B}\)

⇒ \(R=\frac{\rho l}{A}=\frac{4 \rho l}{\pi d^2}\) [4, ρ, l, π – Constant]

∴ \(\frac{R_A}{R_B}=\frac{l_A}{l_B} \times\left(\frac{d B}{d A}\right)^2 = \frac{V_A}{V_{B}}=\frac{1}{2} \times\left(\frac{3}{2}\right)^2 = \frac{V_A}{V_{B}}=\frac{9}{8}\)

CBSE Class 12 Physics Chapter-3 Important Questions

Question 3. Infinity resistance in a resistance box has:

1. A resistance of 105Ω
2. A resistance of 107Ω
3. A resistor of resistance
4. A gap only

Answer: 4. A gap only

Question 4. A battery of 15V and negligible internal resistance is connected across a 50Ω resistor. The amount of energy dissipated as heal to the resistor in one minute is:

1. 122 J
2. 270 J
3. 420 J
4. 720 J

Answer: 2. 270 J

Use \(H=\frac{V^2}{R} t\)

Question 5. In a potentiometer experiment, the balancing length of a cell is 120cm. When the cell is shunted with a 1 Ω resistance, the balancing length becomes 40 cm. The internal resistance of the cell is:

1. 10Ω
2. 7Ω
3. 3Ω
4. 2Ω

Answer: 4. 2Ω

Question 6. Two students A and B calculate the charge flowing through a circuit. A concludes that 300 C of charge flows in 1 minute. B concludes that 3.125 x 10¹⁹ electrons flow in 1 second. If the current measured in the circuit is 5 A, then the correct calculation is done by:

1. A
2. B
3. Both A and Both
4. Neither A nor Both

Answer: 3. Both A and Both

⇒ \(I=\frac{q}{t}\) [for A]

∴ \(I=\frac{ne}{t}\) [for B]

Question 7. The resistances of two wires having the same length and the same area of cross-section arc 2Ω and 8 Ω respectively. If the resistivity of 2Ω wire is 2.65 x 10^-8 m then the resistivity of 8Ω wire is:

1. 10.60 x 10^-4 Ω m
2. 8.32 x 10^-8 Ω m
3. 7.61 x 10^-8 Ωm
4. 5.45 x 10^-8 Ω m

Answer: 1. 10.60 x 10^-4 Ω m

Use \(R=\frac{\rho l}{A}\)

⇒ \(\frac{\rho_2}{\rho_1}=\frac{R_2}{R_1}\)

⇒ \(\rho_2=\frac{8}{2} \times 2.65 \times 10^{-8}\)

∴ \(\rho_2=10.60 \times 10^{-8} \Omega \mathrm{m}\)

CBSE Class 12 Physics Chapter-3 Important Questions

Question 8. The given figure shows an I-V graph of a copper wire of length L and an area of cross-section A. The slope of the curve becomes

1. Less if the length of the wire is increased
2. More if the length of the wire is increased
3. More if a wire of steel of the same dimension is used
4. If the temperature of the wire is increased

Answer: 1. Less if the length of the wire is increased

⇒ \(\frac{I}{V}=\frac{1}{R}=\frac{A}{\rho l}\)

Slope = \(\frac{A}{\rho l}\)

l slope ↓

Question 9. When a potential difference V is applied across a conductor at temperature T. the drift velocity of the electrons is proportional to

1. T
2. √T
3. V
4. √V

Answer: 3. V

∴ \(v_d=\frac{c V}{m l} \bar{\tau}\)

∴ V_d ∝ V

Question 10. A cell supplies a current of 0.9 A through a 20 resistor and a current of 0.3 A through a 70 resistor. What is the internal resistance of cells?

1. 0.5Ω
2. 1.0Ω
3. 1.2Ω
4. 2.0Ω

Answer: 1. 0.5Ω

E = I₁ (R₁ + r) ⇒ E = 0.9(2 + r) →(1)

E = I₂ (R₂ + r) ⇒ E = 0.3 (7 + r) →(2)

From equation (1) and (2)

0.9 (2 + r) = 0.3 (7 + r)

6 + 3r = 7 + r

2r = 1 ⇒ r = 0.5 Ω

Question 11. At what temperature would the resistance of a copper conductor be double its resistance at 0°C? Given temperature coefficient of resistance for copper is 3.9 x 10^-3 °C^-1.

1. 256.4°C
2. 512.8°C
3. 100°C
4. 256.4 K

Answer: 1. 256.4°C

R₁ = R₀ (1 +∝ t)

2R₀ = R₀(1 + 3.9 x 10^-3 x t) ⇒ \(\mathrm{t}=\frac{2-1}{0.0039}\) = 256.4°C

Question 12. A student is asked to connect four cells of emf e each and internal resistance r each in a series of helping conditions. By mistake, he oppositely connects one cell. What will be the effective EMF and effective internal resistance?

1. 4ε, 2r
2. 2ε, 4r
3. 3ε, 2r
4. 4ε, 4r

Answer: 2. 2ε, 4r

Question 13. In a hydrogen atom, the electron is moving in a circular orbit of radius 5.0 x 10^-11 m with a constant speed of 2 x 10⁶ m/s. The electric current formed due to the motion of electrons is _______.

1. 1.12 A
2. 1.02 A
3. 1.02 mA
4. 1.12 mA

Answer: 3. 1.02 mA

∴\(I=\frac{e V}{2 \pi r} ⇒ \) \(I=\frac{1.6 \times 10^{-19} \times 2 \times 10^6}{2 \times 3.14 \times 5 \times 10^{11}} \mathrm{~A}\) ⇒ I = 1.02 mA

CBSE Class 12 Physics Chapter-3 Important Questions

Question 14. A voltmeter of very high resistance is joined in the circuit as shown in the figure. The voltage shown by the voltmeter will be _________.

1. 5 V
2. 2.5 V
3. 10 V
4. 7.5 V

Answer: 1. 5 V

⇒ \(I=\frac{10}{5+5}=1 \mathrm{~A}\)

∴ V = IR = 1 x 5 = 5V

Question 15. The figure shows a part of a closed circuit. If the current flowing through it is 2A. What will be the potential difference between points B and A, V_B– V_A is:

image

1. +2V
2. +1 V
3. -1V
4. -2V

Answer: 4. -2V

Apply KVL

image

⇒ \(2 \times \frac{1}{4}+1+2 \times \frac{1}{4}=V_A-V_B\)

⇒ 2 = V_A-V_B

∴ V_B-V_A = -2V

Question 16. If the current in an electric bulb increases by 2%. what will be the change in the power of a bulb? (Assume that the resistance of the filament of a bulb remains constant).

1. Decreases by 2%
2. Decreases by 4%
3. Increases by 2%
4. Increases by 4%

Answer: 4. Increases by 4%

P = I²R

⇒ \(\frac{\Delta \mathrm{P}}{\mathrm{P}} \times 100=2 \frac{\Delta \mathrm{I}}{\mathrm{I}} \times 100\), R constant

⇒ 2 x 2

⇒ \(\frac{\Delta P}{P} \times 100=4\)

So power will increase by 4%.

Important Questions in Physics Class 12 – Current Electricity

Question 17. Two bulbs of 220 V and 100 W arc first connected in parallel and then in series with a supply of 220 V. Total power in both cases will be ______ respectively.

1. 100 W. 50 W
2. 50 W. 100 W
3. 200 W. 50 W
4. 50 W. 200 W

Answer: 3. 200 W. 50 W

In parallel → P = P₁ + P₂

P= 200 W

∴ Series \(\frac{1}{P}=\frac{1}{P_1}+\frac{1}{P_2}\)

So, P = 50 W

Question 18. Kirchhoff’s junction rule represents ________.

1. Conservation of energy
2. Conservation of linear momentum
3. Conservation of angular momentum
4. Conservation of charge

Answer: 4. Conservation of charge

Question 19. The device has powder P and voltage ‘V’. The connecting wires from the power station to the device have a finite resistance RC. The power dissipated in the connecting wires PC.

1. \(\frac{V^2 R_C}{P}\)
2. \(\frac{\mathrm{PR}_{\mathrm{C}}^2}{\mathrm{~V}}\)
3. \(\frac{P^2 R_C}{V^2}\)
4. \(\frac{V R_C}{P^2}\)

Answer: 3. \(\frac{P^2 R_C}{V^2}\)

Current following

∴ \(I=\frac{P}{V}\)

So power loss across the wire, Pe = I²RC

∴ \(P_e=\frac{P^2 R_e}{V^2}\)

Question 20. Dimension of mobility (μ) is _______.

1. M^-1T²A^-1
2. M¹L³T^-3A^-2
3. M¹L³T^-4A^-1
4. M¹L⁴T^-3A^-1

Answer: 1. M^-1T²A^-1

Important Questions in Physics Class 12 – Current Electricity Assertion And Reason

For question numbers 1 to 4 two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (1). (2). (3) and (4) as given below.

1. Both A and R are true and R is the correct explanation of A
2. Both A and R are true but R is NOT the correct explanation of A
3. A is true but R is false
4. A is false and R is also false

Question 1. Assertion: The total current entering a circuit is equal to that leaving it by Kirchhoff’s law.

Reason: It is based on the conservation of charge.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 2. Assertion: The terminal potential of a cell is always less than its emf.

Reason: Potential drop due to internal resistance of cell increases the terminal potential difference.

Answer: 4. A is false and R is also false

Question 3. Assertion: The connecting wires are made of copper.

Reason: The electrical conductivity of copper is high.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 4. Assertion: There is no current in the metal in the absence of an electric field.

Reason: The motion of free electrons occurs randomly.

Answer: 1. Both A and R are true and R is the correct explanation of A

Class 12 Physics Current Electricity Short Answer Questions

Question 1. The variation of the drift velocity (v_d) of electrons in two copper wires A and B of different lengths versus the potential difference (V) applied across their ends

1. What does the slope of the line represent?
2. Which one of the two wires is longer?

Answer:

V_d = μE, V = El

⇒ \(\mathrm{v}_{\mathrm{d}}=\frac{\mu \mathrm{V}}{l}\)

⇒ \(v_{\mathrm{d}}=\left(\frac{\mu}{l}\right) \mathrm{V}\)

compare with y = mx

1. Slope = \(\) = mobility of charge carriers
2. For constant potential difference (V_d)_A > (V_d)_B

That’s why B has a longer wire.

Question 2. Two wires X and Y of the same material and equal lengths having areas of cross-section A and 2A respectively, are connected in parallel across an ideal battery of emf E. What is the ratio of current density (J_X/J_Y) in them?

Answer:

⇒ \(J=\frac{I}{A}=\frac{E}{R A}\)

⇒ \(\mathrm{J}=\frac{\mathrm{E}}{\rho \ell} \times \frac{\mathrm{A}}{\mathrm{A}}\) (\(\mathrm{R}=\frac{\rho \mathrm{l}}{\mathrm{A}}\))

∴ \(J=\frac{E}{\rho l}\)

So, for both wires, E, ρ, and l are the same

∴ \(\frac{\mathrm{J}_x}{\mathrm{~J}_y}=1: 1\)

Question 3. When 5V potential difference is applied across a wire of length 0. 1 m. the drift speed of electrons is 2.5 x 10^-4 m/s. If the electron density in the wire is 8 x 10²⁸m^-3 calculate the resistivity of the material of the wire.

Answer:

Given: V = 5V

Length of wire l = 0.1m

v_d = 2.5 x 10^-4 m/s

Electron density n = 8 x 10²⁸ m^-3

We know the drift velocity and current are related by the formula

i = ne A v_d → (1)

Where n is the electron density, and e is the charge on an electron. A is an area of the cross-section and v_d is drift velocity.

Also, i = V/R and R = ρl/A where p is resistivity. l is the length of the conductor

so, i = VA/ρl → (2)

comparing equation (1) and (2) we get.

VA / ρl = ne A V_d

or ρ = V / ne l v_d

Put values of all.

ρ = 5/0.1 x 8 x 10²⁸ x 1.6 x 10^-19 x 2.5 x 10^-4

ρ = 1.56 x l0^-5 ohm-meter

Question 4. A battery of emf 12 V and internal resistance 2 Ω is connected to a 4 Ω resistor as shown in the figure.

1. Show that a voltmeter when placed across the cell and the resistor, in turn, gives the same reading.
2. To record the circuit’s voltage and current, why is the voltmeter placed in parallel and the ammeter in series in the circuit?

Answer:

1. When the voltmeter is connected across the cell

I = E/(R + r ) = 12 /(2 + 4) = 12/6 = 2 A

V₁= E-Ir = 12- (2 x 2 ) = 8 V

When the voltmeter is connected across the resistor

V₂ = ER /(r + R) = ( 12 x 4)/(4 + 2) = 12 x 4/6 = 8 V

So, v₁ = v₂

2. A Voltmeter is used to measure the potential difference across two points in a circuit since the voltage in the branches remains the same in a parallel connection. also the resistance of the voltmeter is very high due to which a very small current flows through the voltmeter so it is connected in parallel to measure the voltage.

An ammeter is used to measure the current flowing through a component/circuit. Since the current remains the same in series connections and also the resistance of an ammeter is very small it doesn’t affect the current to be measured. So an ammeter is connected in series to measure current.

Question 5. Two cells of EMFs 1.5 V and 2.0 V having internal resistance 0.2 Ω. and 0.3 Ω respectively are connected in parallel. Calculate the cnif and internal resistance of the equivalent cell.

Answer:

Given E₁ = 1.5 V and r₁ = 0.2 Ω

E₂ = 2 V and r₂ = 0.3 Ω

Equivalent emf = \(\frac{E_1 r_2+E_2 r_1}{r_1+r_2}=\frac{1.5 \times 0.3+2 \times 0.2}{0.5}=\frac{0.85}{0.5}=1.7 \mathrm{~V}\)

∴ Equivalent resistance = \(\frac{r_1 r_2}{r_1+r_2}=\frac{0.2 \times 0.3}{0.2+0.3}=\frac{0.06}{0.5}=0.12 \Omega\)

r_eq, = 0.12 Ω

Question 6.

1. Define the term ‘relaxation time’ in a conductor.
2. Define the mobility of a charge carrier. What is its relation with relaxation lime?

Answer:

1. Relaxation time is the average time interval between two successive collisions of an electron in a conductor when current flows.
2. Mobility of a charge carrier is defined as the drift velocity of the charge carrier per unit electric field i.e μ = v_d/E = eτ/m

Question 7. A metal rod of square cross-sectional area A having length ( has current 1 flowing through it and a potential difference of V volt is applied across its ends. Now the rod is cut parallel to its length into two identical pieces and joined as shown in Figure 2, What potential difference must be maintained across the length 2l so that the current in the rod is still 1?

Answer:

As, \(V=I R=\frac{I_\rho l}{A}\)

Now, \(\frac{V_{\text {new }}}{V}=\frac{l_{\text {new }}}{A_{\text {new }}} \times \frac{A}{l}=\frac{2}{1/2}\) OR V_new = 4V

Now 4V potential difference must be maintained across the length 2l to maintain the same current in the rod.

Question 8. Two wires one of copper and the other of manganin have the same resistance and equal length. Which wire is thicker and why?

Answer:

Manganin is an alloy of Cu with manganese and nickel. Since manganese and nickel have a resistivity greater than copper, pure copper has lower resistivity as compared to alloy manganin. For the same resistance and equal length, manganin wire is thicker than copper.

∴ \(R=\rho \frac{l}{A} \Rightarrow \rho=\frac{R A}{l}\) (∵ \(\rho \propto A\))

Question 9. The plot of the variation of potential difference across a combination of three identical cells in series, versus current is shown below. What is the emf and internal resistance of each cell?

Answer:

V = Terminal voltage across cell combination

The terminal voltage across a cell can be obtained by subtracting the potential drop across the internal resistance of the cell from the emf of the cell.

V = E – IR

When I = 0, = V = E

From graph it is found that when I = 0, V = 6V ⇒ E = 6V

As I = 1A, V = 0 from graph

As V = E-Ir ⇒ 0 = 6-1.r => 6 = 1.r

r = 6 Ω

As 3 identical cells are connected in series so EMF and internal resistance of each cell are 2V and 2 Ω respectively.

Question 10.

1. Derive an expression for the drift velocity of free electrons.
2. How does the drift velocity of electrons in a metallic conductor vary with an increase in temperature? Explain.

Answer:

1. Drift velocity is defined as the average velocity with which free electrons in a conductor drift in a direction opposite to the direction of the applied electric field. When a conductor is subjected to an electric field E. each electron experiences a force.

⇒ \(\vec{F}=-\mathrm{e} \vec{E}\)

and acquires an acceleration

⇒ \(\mathrm{a}=\frac{\overrightarrow{\mathrm{F}}}{\mathrm{m}}=\frac{-\mathrm{e} \overrightarrow{\mathrm{E}}}{\mathrm{m}}\) → (1)

Here m = mass of the electron, e = charge. E = electric field. The average time difference between two consecutive collisions is known as the relaxation time of an electron.

⇒ \(\tau=\frac{\tau_1+\tau_2+\ldots \ldots+\tau_n}{n}\) → (2)

As v = u + at (from equations of motion)

The drift velocity v_d is defined as

⇒ \(\vec{v}_{\mathrm{d}}=\frac{\vec{v}_1+\vec{v}_2+\ldots+\vec{v}_n}{n}\)

⇒ \(\overrightarrow{\mathrm{v}}_{\mathrm{d}}=\frac{\left(\overrightarrow{\mathrm{u}}_1+\overrightarrow{\mathrm{u}}_2+\ldots .+\overrightarrow{\mathrm{u}}_{\mathrm{n}}\right)+\mathrm{a}\left(\tau_1+\tau_2+\ldots .+\tau_{\mathrm{n}}\right)}{\mathrm{n}}\)

⇒ \(\vec{v}_d=0+\frac{a\left(\tau_1+\tau_2+\ldots .+\tau_n\right)}{n}\)

(∵ average thermal velocity = 0)

∴ \(\overrightarrow{\mathrm{v}}_{\mathrm{d}}=0+\mathrm{at}\)

⇒ \(\overrightarrow{\mathrm{v}}_{\mathrm{d}}=-\left(\frac{\mathrm{e} \overrightarrow{\mathrm{E}}}{\mathrm{m}}\right) \tau\) ⇒ (\(\left|\vec{v}_{\mathrm{d}}\right|=\left(\frac{e \tau}{m}\right) \vec{E}\))

2. According to the drift velocity expression, relaxation time is the time interval between successive collisions of an electron. On increasing temperature, the electrons move faster and more collisions occur more quickly. Hence, relaxation lime decreases with an increase in temperature which implies that drift velocity also decreases with temperature.

Question 11. Two identical cells of cmf 1.5 V each joined in parallel to supply energy to an external circuit consisting of two resistances of 7 Ω each joined in parallel. A very high resistance voltmeter reads the terminal voltage of cells to be 1.4 V. Calculate the internal resistance of each cell.

Answer:

A high resistance voltmeter means that no current flows through the voltmeter (practically very little current). When two batteries are connected in parallel, then

⇒ \(E_{eq}=\frac{E_1 r_2+E_2 r_1}{r_1+r_2}\)

Here r₁ = r₂ = r

E₁ = E₂ = I.5V (given)

⇒ \(\mathrm{E}_{\mathrm{eq}}=\frac{1.5 \times \mathrm{r}+1.5 \times \mathrm{r}}{2 \mathrm{r}}\)

E_eq = 1.5 V

Now \(\left.\begin{array}{l}
\mathrm{R}_1=7 \Omega \mathrm{R}_2=7 \Omega
\end{array}\right] \text { given }\)

So \(\frac{1}{R_{\mathrm{eq}}}=\left(\frac{1}{7}+\frac{1}{7}\right) \Omega\)

⇒ \(\mathrm{R}_{\mathrm{eq}}=\frac{7}{2}=3.5 \Omega\)

∵ \(I=\frac{\text { terminal voltage }}{\text { equivalent resistance }}\)

V = terminal voltage = 1.4 (given) = voltmeter reading

So, \(I=\frac{1.4}{3.5}=0.4 \mathrm{~A}\)

Now V = E_eq– 1 x r_eq ⇒ 1.4= 1.5- 0.4 x r_eq

0.4 x r_eq = 0.1

As r_eq = r/2 (∵ \(\frac{1}{r_{e q}}=\frac{1}{r}+\frac{1}{r}\))

So r of each cell = 0.5Ω

Question 12.

1. Define the term ‘conductivity’ of a metallic wire. Write it’s ST unit.
2. Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxation lime. Hence obtain the relation between current density and the applied electric field \(\vec{E}\).

Answer:

1. The conductivity of a material equals the reciprocal of the resistance of its wire of unit length and unit area of cross-section.

Alternatively:

The conductivity (σ) of a material is the reciprocal of its resistivity (ρ)

(Also acept \(\sigma=\frac{1}{\rho}\))

Its SI Units (\(\frac{1}{\text { olnm-metrc }}\)) or hom^-1m^-1 or (mho m^-1) or sciemen m^-1.

2. The Acceleration, \(\vec{a}=-\frac{e}{m} \vec{E}\)

The average drift velocity, V_d, is given by \(\vec{v}_{\mathrm{d}}=-\frac{\mathrm{e} \vec{\mathrm{E}}}{\mathrm{m}} \tau\)

(τ = average time between collisions or average relaxation lime)

If n is the number of free electrons per unit volume, then-current I is given by

⇒ \(I=n e A\left|v_d\right|\)

⇒ \(I=n e A\left(\frac{e \tau}{m}\right) E = I=\left(\frac{n e^2 \tau}{m}\right) E A\) (\(v_{\mathrm{d}}=\left(\frac{\mathrm{e} \tau}{\mathrm{m}}\right) \mathrm{E}\))

But I = J A (J = current density)

We, therefore, get

⇒ \(\mathrm{J}=\frac{\mathrm{ne}^2}{\mathrm{~m}} \tau \mathrm{E}\), The term \(\frac{n e^2}{m} \tau\) is conductivity.

∴ \(\sigma=\frac{\mathrm{ne}^2 \tau}{\mathrm{m}}\) ⇒ J = σE

Question 13.

Use Kirchhoff’s rules, to calculate the current in the arm AC of the given circuit.

Answer:

Applying Kirchhoff’s junction rule at node A

I₃ = I₁+I₂ → (1)

Applying Kirchhoff’s KVL in loop EFCAE

-30 I₁+40-40 I₃ = 0

3 I₁+4 I₃ = 4 → (2)

Applying KVL in loop EFDBE

-30 I₁+20 I₂ – 80 = 0

-3 I₁ + 2 I₂ = 8 → (3)

from eq (1) we put the value of I₃ in eq (2)

3 I₁ +4(I₁ + I₂) = 4

7 I₁ +4 I₂ = 4 → (4)

from eq (3) and (4) we get

I₁ =-12/13 A

Putting I₁ in eq (4) we get

⇒ \(\mathrm{I}_2=\frac{34}{13} \mathrm{~A}\)

Then form eq(1) we get \(\mathrm{I}_3=\frac{22}{13} \mathrm{~A}\)

Question 14.

1. The potential difference applied across a given resistor is altered so that the heat produced per second increases by a factor of 9. By what factor does the applied potential difference change?
2. In the figure shown, an ammeter A and a resistor of 4 Ω are connected to the terminals of the source. The emf of the source is 12 V having an internal resistance of 2 Ω. Calculate the voltmeter and ammeter readings.

Answer:

1. \(\mathrm{H}=\frac{\mathrm{V}^2}{\mathrm{R}} \mathrm{t}\) (initially) →(1)

After altering potential differences, we can write,

⇒ \(H^{\prime}=\frac{V^{\prime 2}}{R} t\)

∵ H’ = 9H we get,

⇒ \(9 \mathrm{H}=\frac{\mathrm{V}^{\prime 2}}{\mathrm{R}} \mathrm{t}\) → (2)

Solving (1) and (2) we get, V’ = 3V

2.

Total current ‘I’ in the circuit, \(I=\frac{E}{R+r}=\frac{R}{4+2}=2 A\)

Now potential differences across batteries is

V + Ir = E

V + 2 x 2 = 12

∴ V = 8 Volt

Class 12 Physics Current Electricity Long Answer Questions

Question 1. Wheatstone bridge is an arrangement of four resistances P, Q, R, and S connected as shown in the figure. Their values are so adjusted that the galvanometer G shows no deflection. The bridge is then said to be balanced when this condition is achieved. In the setup shown here, points B and D are at the same potential and it can be shown that P/Q = R/S This is called the balancing condition. If any three resistances are known, the fourth can be found. The practical form of the Wheatstone Bridge is a slide wire bridge or Meter Bridge. Using this the unknown resistance can be determined as \(S=\left(\frac{100-\ell}{\ell}\right) \times R\), where l is the balancing length of the meter bridge.

(1). In a Wheatstone bridge circuit, P = 5 Ohm, Q = 6 Ohm, R = 10 Ohm and S = 5 Ohm. What is the value of additional resistance to be used in series with S, so that the bridge is balanced?

1. 9 Ohm
2. 7 Ohm
3. 10 Ohm
4. 5 Ohm

Answer: 2. 7 Ohm

(2). A Wheatstone bridge consisting of four arms of resistance P, Q, R, S is most sensitive when

1. All the resistance is equal
2. All the resistance is unequal
3. The resistance P and Q arc equal but R>>P and S>>Q
4. The resistance P and Q are equal but R<<P and S<<Q

Answer: 1. All the resistance is equal

(3). The percentage error in measuring resistance with a meter bridge can be minimized by adjusting the balancing point close to

1. 0
2. 20 cm
3. 50 cm
4. 80 cm

Answer: 3. 50 cm

(4). In the meter bridge experiment, the ratio of the resistance of the left and light gap is 2 : 3. The balance point from the left is

1. 20 cm
2. 50 cm
3. 40 cm
4. 60 cm

Answer: 3. 40 cm

2. Relation between V, E, and r of a cell

Emf of a cell is the potential difference between two electrodes of the cell when no current is drawn from the cell. Internal resistance is the resistance offered by the electrolyte of a cell when the electric current flows through it. The internal resistance of a cell depends upon the following factors:

1. Distance between the electrodes
2. Nature and temperature of the electrolyte
3. Nature of electrodes
4. Area of electrodes.

For a freshly prepared cell, the value of internal resistance is generally low and goes on increasing as the cell is put to more use. The potential difference between the two electrodes of a cell in a closed circuit is called terminal potential difference and its value is less than the emf of the cell during discharging and more than the emf of the cell during charging of the cell in a closed circuit. It can be written as V = E – Ir or V = E + Ir

(1). The terminal potential difference of two electrodes of a cell is equal to cmf  the cell when

1. 1 ≠ 0
2. 1 = 0
3. Both (1) and (2)
4. Neither (1) and (2)

Answer: 2. Both (1) and (2)

(2). A cell of cmf E and internal resistance r gives a current of 0.5 A with an external resistance of 12 Ohm and a current of 0.25 A with an external resistance of 25 Ohm. What is the value of the internal resistance of the cell?

1. 5 Ohm
2. 1 Ohm
3. 7 Ohm
4. 3 Ohm

Answer: 2. 1 Ohm

(3). If external resistance connected to a cell has been, increased to 5 times, the potential difference across the terminals of the cell increases from 10 V to 30 V. Then the cmf of the cell is

1. 30 V
2. 60 V
3. 50 V
4. 40 V

Answer: 60 V

(4). During the charging of the cell the correct relation is

1. E = V + Ir
2. E = V – Ir
3. V = E + Ir
4. V = E – Ir

Answer: 3. V = E + Ir

3. A battery is a combination of two or more cells. In the following figure, a single battery is represented in which two cells of emf ε₁, and ε₂, and internal resistance r₁ and r₂ respectively are connected.

Answer the following Questions:

(1). The equivalent emf of this combination is:

1. \(\frac{\varepsilon_1 r_1+\varepsilon_2 r_2}{r_1+r_2}\)
2. \(\frac{\varepsilon_1 r_1-\varepsilon_2 r_2}{r_1+r_2}\)
3. \(\frac{\varepsilon_1 r_2-\varepsilon_2 r_1}{r_1+r_2}\)
4. \(\varepsilon_1-\varepsilon_2\)

Answer: 3. \(\frac{\varepsilon_1 r_2-\varepsilon_2 r_1}{r_1+r_2}\)

(2). For terminalB to be negative:

1. \(\varepsilon_1 r_2>\varepsilon_2 r_1\)
2. \(\varepsilon_1 r_2<\varepsilon_2 r_1\)
3. \(\varepsilon_1 r_1>\varepsilon_2 r_2\)
4. \(\varepsilon_2 r_2=\varepsilon_1 r_1\)

Answer: 2. \(\varepsilon_1 r_2<\varepsilon_2 r_1\)

(3). The current in the internal circuit is

1. \(\frac{\varepsilon_1+\varepsilon_2}{r_1+r_2}\)
2. \(\frac{\varepsilon_1-\varepsilon_2}{r_1+r_2}\)
3. \(\frac{\varepsilon_1}{r_1}-\frac{\varepsilon_2}{r_2}\)
4. \(\frac{\varepsilon_1}{r_2}-\frac{\varepsilon_2}{r_1}\)

Answer: 1. \(\frac{\varepsilon_1+\varepsilon_2}{r_1+r_2}\)

(4). The equivalent internal resistance of the combination is:

1. \(\frac{r_1+r_2}{r_1 r_2}\)
2. \(r_1+r_2\)
3. \(\frac{r_1 r_2}{r_1+r_2}\)
4. \(r_1-r_2\)

Answer: 3. \(\frac{r_1 r_2}{r_1+r_2}\)

Question 4.

1. Define the term drift velocity.
2. Based on electron drift, derive an expression for the resistivity of a conductor in terms of the number density of free electrons and relaxation lime. On what factors do the resistivity of a conductor depend?
3. Why are alloys like Constantan and manganin arc used for making standard resistors?

Answer:

1. Drift velocity is defined as the average velocity with which the electrons drift towards the positive terminal under the effect of the applied electric field.

2. We know that the current flowing through the conductor is:

I = n A e v_d

∴ \(\mathrm{l}=\mathrm{neA}\left(\frac{\mathrm{eE \tau}}{\mathrm{m}}\right)\)

Using \(E=\frac{V}{l}\)

⇒ \(I=n e A\left(\frac{e V}{m l}\right) \tau=\left(\frac{n e^2 A \tau}{m /}\right) V=\frac{1}{R} V\)

I ∝ V → which is Ohm’s law

Where \(R=\frac{m l}{n A e^2 \tau}\) is constant for a particular temperature and is called the resistance of the conductor.

∴ \(R=\left(\frac{m}{n e^2 \tau}\right) \frac{l}{A}=\frac{\rho l}{A} \Rightarrow \rho=\left(\frac{m}{n e^2 \tau}\right)\)

Where ρ is the specific resistance or resistivity of the material of the wire. It depends on the number of free electrons per unit volume and temperature

3. Alloys like constantan and manganin are used for making standard resistors, because:

• They have a high value of resistivity and
• The temperature coefficient of resistance is negligible

Question 5.

1. Plot a graph showing the variation of voltage v/s the current drawn from the cell. How can one get information from this plot about the cmf of the cell and its internal resistance?
2. Two cells of cmf’s E₁, and E₂, and internal resistance r₁, and r₂ arc connected in parallel. Obtain the expression for the emf and internal resistance of a single equivalent cell that can replace this combination.

Answer:

1. The terminal potential difference across the cell,

V = E – Ir or V = – rl + E

Comparing the above relation with the equation of a straight line i.e. y = mx + c, it follows that the graph between (along the x-axis) and V (along the y-axis) will be a straight line having a slope equal to -r and making intercept equal to E on the y-axis. Thus we get information about the EMF of the cell and its internal resistance from this plot.

2.

I = I₁ + I₂ → (1)

v = V_B1-V_B2

V = Polcnlial difference across terminal B₁ and B₂

V = E₁ – I₁r₁ – for first cell

V = E₂ – I₂r₂ – for second cell

and I = I₁ + I₂ as per above eq(1)

So \(I=\frac{E_1-V}{r_1}+\frac{E_2-V}{r_2}=\left(\frac{E_1}{r_1}+\frac{E_2}{r_2}\right)-V\left(\frac{1}{r_1}+\frac{1}{r_2}\right)\) → (2)

\(I=\frac{E_{eq .}-V}{r_{eq .}}\) → (3)

By equation (2) and (3)

⇒ \(\frac{E_{eq .}-V}{r_{eq .}}=\left(\frac{E_1}{r_1}+\frac{E_2}{r_2}\right)-V\left(\frac{1}{r_1}+\frac{1}{r_2}\right)\)

Now, \(\frac{1}{r_{eq}}=\frac{1}{r_1}+\frac{1}{r_2}\) and \(\frac{E_{eq}}{r_{eq}}=\frac{E_1}{r_1}+\frac{E_2}{r_2}\)

∴ \(E_{eq}=\frac{E_1 r_2+E_2 r_1}{r_1+r_2}\) and \(r_{eq}=\frac{r_1 r_2}{r_1+r_2}\)

CBSE Class 12 Physics Chapter 4 Moving Charges And Magnetism Multiple Choice Question And Answers

Question 1. The moving coil galvanometer G₁ and G₂ have the following particulars respectively:

N₁ = 30 , A₁ = 3.6 x 10^-3m² , B₁ = 0.25 T

N₂ = 42 , A₂ = 1.8 x 10^-3m², B₂ = 0.50 T

The spring constant is the same for both the galvanometers, The ratio of current sensitivities of G₁ and G₂ is:

1. 5:7
2. 7:5
3. 1:4
4. 1:1

Answer: 1. 5:7

Read and Learn More Important Questions for Class 12 Physics with Answers

⇒ \(\frac{\mathrm{I}_{\mathrm{S}_1}}{\mathrm{I}_{\mathrm{S}_2}}=\frac{\mathrm{N}_1 \mathrm{~A}_1 \mathrm{~B}_1}{\mathrm{~K}_1} \times \frac{\mathrm{K}_2}{\mathrm{~N}_2 \mathrm{~A}_2 \mathrm{~B}_2}\)

K₁ = K₂

So \(\left(\frac{N_1}{N_2}\right)\left(\frac{A_1}{A_2}\right)\left(\frac{B_1}{B_2}\right)\)

= \(\frac{30}{42} \times \frac{3.6 \times 10^{-3}}{1.8 \times 10^{-3}} \times \frac{0.25}{0.50}\)

= \(\frac{5}{7} \times 2 \times \frac{1}{2}\)

= 5:7

CBSE Class 12 Physics Chapter 4 Question 2. A current 1 is flowing through the loop as shown in the figure ( MA = R, MB = 2R ). The magnetic field at the center of the loop is \(\left(\frac{\mu_0 I}{R}\right)\) times:

1. \(\frac{5}{16}\) in to the plane of paper
2. \(\frac{5}{16}\) Out to the plane of paper
3. \(\frac{7}{16}\) in to the plane of paper
4. \(\frac{7}{16}\) out to the plane of paper

Answer: 4. \(\frac{7}{16}\) out to the plane of paper

B = B_DA(x)+B_AC(x)

= \(\frac{3}{4} \times \frac{\mu_0 \mathrm{I}}{2 \mathrm{R}}+\frac{1}{4} \times \frac{\mu_0 \mathrm{I}}{2(2 \mathrm{R})}\)

= \(\frac{3}{8} \frac{\mu_0 I}{R}+\frac{1}{16} \frac{\mu_0 I}{R}\)

= \(\frac{\mu_0 \mathrm{I}}{\mathrm{R}}\left(\frac{3}{8}+\frac{1}{16}\right)\)

= \(\frac{\mu_0 I}{R}\left(\frac{6+1}{16}\right)\)

B = \(\frac{7}{16} \frac{\mu_0 I}{R}\)

Question 3. A long straight wire in the horizontal plane carries a current of 15A in north to south direction. The magnitude and direction of the magnetic field at a point 2.5 m east of the wire respectively are:

1. 1.2 μT, vertically upward
2. 1.2 μT, vertically downward
3. 0.6 μT, vertically upward
4. 0.6 μT vertically downward

Answer: 1. 1.2 μT, vertically upward

B = \(\frac{\mu_0 \mathrm{I}}{2 \pi \mathrm{r}}=\frac{4 \pi \times 10^{-7} \times 15}{2 \pi \times 2.5}=1.2 \mu \mathrm{T}\) (Vertically upwards)

CBSE Class 12 Physics Chapter 4 Question 4. An electron is projected with velocity \(\vec{V}\) along the axis of a current carrying a long solenoid. Which of the following statements is true?

1. The path of the electron will be circular about the axis
2. The electron will be accelerated along the axis
3. The path of the electron will be helical
4. The electron will continue to move at the same velocity v along the axis of the solenoid.

Answer: 4. The electron will continue to move at the same velocity v along the axis of the solenoid.

Question 5. If the speed v of a charged particle moving in a magnetic field \(\vec{B}\) (\(\vec{v}\) is perpendicular to \(\vec{B}\)) is halved, then the radius of its path will:

1. Not change
2. Become two times
3. Become one-fourth
4. Become half

Answer: 4. Become half

∴ \(r=\frac{m v}{q B}\)

Question 6. Which of the following is not affected by the presence of a magnetic field?

1. A current-carrying conductor
2. A moving charge
3. A stationary charge
4. A rectangular current loop with its plane parallel to the field

Answer: 3. A stationary charge

Question 7. Identical thick wires and two identical thin wires, all of the same material and the same length form a square in three different ways P, Q, and R as shown. Due to the current in these loops, the magnetic field at the center of the loop will be zero with ease of

1. P and R only
2. Q and R only
3. P and Q only
4. P, Q, and R

Answer: 1. P and R only

Question 8. A circular coil carrying a certain current produces a magnetic field B₀ at its center. The coil is now rewound to have three turns and the same current is passed through it. The magnetic field at the center is

1. 3B₀
2. \(\frac{B_0}{3}\)
3. \(\frac{B_0}{9}\)
4. 9B₀

Answer: 4. 9B₀

Lel coil is of N turns and radius R, \(B_0=\frac{\mu_0 I}{2 R}\)

2πR = length of wire

Now, 2R = 3 x 2πR’

So, \(R^{\prime}=\frac{R}{3}\)

∴ \(B^{\prime}=\frac{\mu_0 I \times 3}{2\left(\frac{R}{3}\right)}=9\left(\frac{\mu_0 I}{2 R}\right)=9 B_0\)

CBSE Class 12 Physics Chapter 4Question 9. A long solenoid carrying current produces a magnetic field B along its axis, if the number of turns in the solenoid is halved and the current in it is doubled, the new magnetic field will be:

1. B/2
2. B/2
3. 2B
4. 4B

Answer: 2. B/2

⇒ \(\overrightarrow{\mathrm{F}}=\mathrm{q}(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})\)

⇒ \(\overrightarrow{\mathrm{F}}=1.6 \times 10^{-19}[(4 \hat{\mathrm{i}}+3 \hat{\mathrm{k}}) \times(3 \hat{\mathrm{k}}+4 \hat{\mathrm{i}})]\)

⇒ \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
4 & 0 & 3 \\
4 & 0 & 3
\end{array}\right|\)

⇒ \(\hat{\mathrm{i}}(0)-\hat{\mathrm{j}}(12-12)+\hat{\mathrm{k}}(0)\)

= 0

So, \(\overrightarrow{\mathrm{F}}=0\)

Question 10. A current-carrying square loop is suspended in a uniform magnetic field acting in the plane of the loop. If the force on one arm of the loop is F, the net force on the remaining three arms of the loop will be:-

1. \(3{\vec{F}}\)
2. \(-3{\vec{F}}\)
3. \({\vec{F}}\)
4. \(-\vec{F}\)

Answer: 4. \(-\vec{F}\)

Question 11. The electron performs circular motion in a circle of radius r, perpendicular to a uniform magnetic field B. The kinetic energy gained by this electron in half the revolution is __________.

1. \(\frac{1}{2} m v^2\)
2. \(\frac{1}{4} m v^2\)
3. Zero
4. πrBeV

Answer: 3. Zero

Work done is zone

Because v ⊥ B

So ΔK = W = 0.

Question 12. At a place, an electric field and a magnetic field are in a downward direction. There an electron moves in a downward direction. Hence this electron.

1. Will bend towards left
2. Will bend towards the right
3. Will gain velocity
4. Will lose velocity

Answer: 4. Will lose velocity

Question 13. When a charged particle moves in a magnetic field its kinetic energy.

1. Remains Constant
2. Increases
3. Can decrease
4. Become zero

Answer: 1. Remains Constant

Question 14. A charged particle moves with velocity v in a uniform magnetic field B. The magnetic force acting on it will be maximum when.

1. \(\vec{V}\) and \(\vec{B}\) arc in same direction.
2. \(\vec{V}\) and \(\vec{B}\) are in opposite direction.
3. \(\vec{V}\) and \(\vec{B}\) are mutually perpendicular.
4. \(\vec{V}\) and \(\vec{B}\) make an angle of 45° with each other.

Answer: 3. \(\vec{V}\) and \(\vec{B}\) are mutually perpendicular.

Question 15. There are 100 turns per cm length in a very long solenoid. It carries a current of 2.5 A. The magnetic field at its center on the axis is __________ T.

1. 3.14 x 10^-2
2. 9.42 x 10^-2
3. 6.28 x 10^-2
4. 12.56 x 10^-2

Answer: 1. 3.14 x 10^-2

B = μ₀ nI

⇒ \(4 \times 3.14 \times \frac{100}{10^{-2}} \times 2.5 \times 10^{-7}\)

⇒ 3.14 x 10^-2T

Question 16. A toroid wound with 100 turns per m of wire carries a current of 3 A. The core of the toroid is made of iron having relative magnetic permeability μ_r = 5000. The magnetic field inside the iron is __________. (μ₀ = 4π x 10^-7 T mA^-1)

1. 0.15 T
2. 1.5 x 10^-2T
3. 0.47 T
4. 1.88 T

Answer: 4. 1.88 T

B = μ₀ nI

= 5000 x 4 x 3.14 x 10^-7 x 100 x 3

B = 1.88 T

Question 17. Two parallel long thin wires, each carrying current I are kept at a separation r from each other. Hence the magnitude of force per unit length of one wire due to the other wire is _________.

1. \(\frac{\mu_0 I^2}{2 \pi r}\)
2. \(\frac{\mu_0 I^2}{r^2}\)
3. \(\frac{\mu_0 \mathrm{I}}{2 \pi \mathrm{r}}\)
4. \(\frac{\mu_0 \mathrm{I}}{2 \pi \mathrm{r}^2}\)

Answer: 1. \(\frac{\mu_0 I^2}{2 \pi r}\)

Question 18. Two concentric rings are kept in the same plane. The number of turns in both rings is 25. Their radii are 50 cm and 200 cm and they carry electric currents of 0.1 A and 0.2 A respectively, in mutually opposite directions. The magnitude of the magnetic field produced at their center is __________T.

1. 2μ₀
2. 4μ₀
3. \(\frac{10}{4} \mu_0\)
4. \(\frac{5}{4} \mu_0\)

Answer: 4. \(\frac{5}{4} \mu_0\)

⇒ \(\overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{B}}_1+\overrightarrow{\mathrm{B}}_2\)

⇒ \(\frac{\mu_0 N_1 I_1}{2 R_1}-\frac{\mu_0 N_2 I_2}{2 R_2}=\frac{\mu_0 \times 25}{2}\left(\frac{0.1}{0.5}-\frac{0.2}{2}\right)=\frac{5}{4} \mu_0\)

Question 19. The current sensitivity of the galvanometer is inversely proportional to _________.

1. Torsional constant
2. Number of turns
3. Area
4. Magnetic field

Answer: 1. Torsional constant

Question 20. Parallel currents ______ and antiparallel currents _______.

1. Attract, Attract
2. Repel, attract
3. Attract, repel
4. Repel, repel

Answer: 3. Attract, repel

Question 21. A solenoid of length 0.5 m has a radius of 1 cm and it is made up of 500 turns. If the magnitude of the magnetic field inside the solenoid is 6.28 x 10^-3 T then it carries a current of _________ A.

1. 4
2. 5
3. 2
4. 10

Answer: 2. 5

B = μ₀nI

Solve I

I = \(\frac{\mathrm{B}}{\mu_{\mathrm{o}} \mathrm{n}}\left[\mathrm{n}=\frac{\mathrm{N}}{\ell}=\frac{500}{0.5}=1000 \text { turns } / \mathrm{m}\right]\)

∴ \(\frac{6.28 \times 10^{-3}}{4 \pi \times 10^{-7} \times 1000}=5 \mathrm{~A}\)

Moving Charges And Magnetism Assertion And Reason

For question numbers 1 to 7 two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (1). (2). (3) and (4) as given below.

1. Both A and R are true and R is the correct explanation of A
2. Both A and R are true but R is NOT the correct explanation of A
3. A is true but R is false
4. A is false and R is also false

Question 1. Assertion: When a charged particle moves with velocity v in a magnetic field B (v⊥B). the force on the particle does not work.

Reason: The magnetic force is perpendicular to the velocity of the particle.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 2. Assertion: The magnetic moment of the toroid is zero.

Reason: The magnetic field outside the volume of the carrying toroid is zero.

Answer: 2. Both A and R are true but R is NOT the correct explanation of A

Question 3. Assertion: Two charge particles at rest experience only electrostatic force.

Reason: Charges at rest can only produce an electrostatic field.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 4. Assertion: A moving charged particle gets energy from a magnetic field.

Reason: Magnetic force works on moving charged particles.

Answer: 4. A is false and R is also false

Question 5. Assertion: The coil is wound over the metallic frame in a moving coil galvanometer.

Reason: The metallic frame helps in making steady deflection without any oscillation.

Answer: 1. Both A and R are true and R is the correct explanation of A

Question 6. Assertion: When the magnet is brought near iron nails, only translatory force acts on it.

Reason: The field due to a magnet is generally uniform.

Answer: 4. A is false and R is also false

Question 7. Assertion: The higher the range of an ammeter, the smaller its resistance.

Reason: To increase the range of the ammeter, the additional shunt needed to be connected across it.

Answer: 1. Both A and R are true and R is the correct explanation of A.

Moving Charges And Magnetism Short Question And Answers

Question 1.

1. Write the relation for the force acting on a charged particle q moving with velocity \(\vec{v}\) in the presence of a magnetic field \(\vec{B}\).
2. A proton is accelerated through a potential difference V, subjected to a uniform magnetic Held acting normal to the velocity of the proton. If the potential difference is doubled, how will the radius of the circular path described by the proton in the magnetic field change?

Answer:

1. \(\vec{F}=q(\vec{v} \times \vec{B})\)

2. \(r=\frac{m v}{q B}=\frac{\sqrt{2 m(K E)}}{q B}\) [mv = P = \(\sqrt{2 \mathrm{mK}}\)] (K → K.E)

= \(\frac{\sqrt{2 m(q V)}}{q B} r \propto \sqrt{V}\)

Thus if V₂ = 2V₁ = r₂ = √2r₁.

Question 2. In the figure given below, wire PQ is fixed while the square loop ABCD is free to move under the influence of currents flowing in them. State with reason, in which direction does the loop begin to move or rotate?

Answer:

Forces on side AB and CD cancel each other, Now force on AD is attractive due to the similar direction of current, and on side BC force is repulsive due to the opposite direction of current.

As side AD is nearer to wire PQ as compared to BC so force on side AD (attractive) is more than the force on side BC ( repulsive), so square loop ABCD does move towards wire PQ.

Question 3.

1. A proton and an electron traveling along parallel paths enter a region of uniform magnetic field, acting perpendicular to their paths. Which of them will move in a circular path with higher frequency?
2. What can be the cause of the helical motion of a charged particle?

Answer:

1. We know that, frequency

‍ \(v=\frac{\mathrm{q} B}{2 \pi \mathrm{m}} \text { and } \mathrm{m}_{\mathrm{e}}<<\mathrm{m}_{\mathrm{p}}\)

So electrons will move with a higher frequency

2. When a charged particle moves in a uniform external magnetic field, with velocity not perpendicular or parallel to the magnetic field, (Means : 0° < θ < 90°) then the charged particle experiences a force also along with torque and performs the helical motion.

Question 4. Draw the magnetic field lines due to a current passing through a long solenoid.

Answer:

Question 5. Find the condition under which the charged particles moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speed.

Answer:

Consider a charge ’q’ moving with velocity \(\vec{v}\) in the presence of both electric field \(\vec{E}\) and magnetic field \(\vec{B}\) experience a force given as

⇒\(\overrightarrow{\mathrm{F}}=\mathrm{q}(\overrightarrow{\mathrm{E}}+\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})=\overrightarrow{\mathrm{F}}_{E}+\overrightarrow{\mathrm{F}}_{\mathrm{B}}\)

Assume, that \(\vec{E}\) and \(\vec{B}\) are ⊥ to each other and also to the velocity of the particle.

Directions of electric force \(\left(\vec{F}_{E}\right)\) and magnetic force \(\left(\vec{F}_{B}\right)\) are just opposite.

∴ \(\vec{F}=q(E-v B) \hat{j}\)

if magnitudes of electric and magnetic force are equal then, the net force on the particle is zero and it will move undeflected in the fields.

qE = qvB or V = E/B

The above condition is used to select charged particles of a particular velocity.

Question 6.

1. Write the expression for the magnitude of the magnetic force acting on a charged particle moving with velocity v in the presence of magnetic field B.
2. A neutron, an electron, and an alpha particle moving with equal velocities enter a uniform magnetic field going into the plane of the paper as shown. Trace their paths in the field and justify your answer.

Answer:

1. Force acting on a charged particle q which is moving with velocity v in magnetic field B is given by \(\vec{F}=q(\vec{v} \times \vec{B})\)

Fleming’s left-hand rule gives the direction of the force. The direction of the force is perpendicular to the plane containing velocity \(\vec{v}\) and magnetic field \(\vec{B}\).

2. A charged particle experiences a force when it enters the magnetic field. Due to the presence of a magnetic field, the charged particle will move in a circular path because the force is perpendicular to the velocity of the charged particle, required centripetal force will be provided by magnetic force.

The radius of the circular path in which the charged particle is moving is “given by r = mv/qB since v and B are constant so the radius of the path of the particle is proportional to their mass to charge ratio.

Alpha-particle will trace a circular path in an anti-clockwise sense and its deviation will be in the direction of \((\vec{v} \times \vec{B})\)

Nculion will pass without any deviation as the magnetic field does not exert force on the neutral particle.

Electron will trace a circular path in a clockwise sense as its deviation is in the direction opposite to \((\vec{v} \times \vec{B})\) with a smaller radius due to mass or charge.

Question 7. Two long straight parallel conductors are carrying steady current I₁ and I₂ separated by a distance d. if the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other. Obtain the expression for this force. Hence define one ampere.

Answer:

We consider two long conductors X₁ Y₁ and X₂Y₂ placed parallel to each other at a distance of d apart. The current I₁ and I₂ are flowing as shown in the diagram. The magnetic field at point P (on the conductor X₁Y₁ due to current I₂ flowing through the long conductor X₂Y₂) is g given by

⇒ \(\mathrm{B}_2=\frac{\mu_0 \mathrm{I}_2}{2 \pi \mathrm{d}}\) →(1)

According to the right-hand rule, the direction of the magnetic field B₂ at point P is perpendicular to the plane of the paper and in an inward direction. Now, the conductor X₁ Y₁ carrying current I₁ lies in the magnetic field B, produced by the conductor X₂Y₂.

Since F=BIl, the force experienced by the unit length of the conductor X₁Y₁ due to magnetic field B₂ is given by

⇒ \(\mathrm{F}=\mathrm{B}_2 \cdot\left(\mathrm{I}_1 \cdot \ell\right)=\frac{\mu_0 \mathrm{I}_1 \mathrm{I}_2}{2 \pi \mathrm{d}}\) → (2)

or

⇒ \(\frac{F}{l}=\frac{\mu_0 I_1 I_2}{2 \pi d}\)

Applying Fleming’s left-hand rule, it follows that the force F on the conductor X₁Y₁ acts in the plane of the paper and towards the left. If we proceed similarly then it can be proved that the conductor X₂Y₂ experiences an equal force in the plane of the paper but towards the right.

Therefore, the two parallel conductors carrying current in the same direction attract each other.

Definition of Ampere: Let I₁ = I₂ = I A and d = 1 m

Then from eq (1), we have that

F = 2x 10^-7 N/mK

This means that one ampere of current is that much current which when flown through two infinitely long parallel conductors separated by one meter in free space, causes a force of 2 x 10^-7 N per meter on each conductor.

Question 8. A rectangular coil of sides ‘l’ and ‘b’ carrying a current I is subjected to a uniform magnetic field \(\vec{B}\) acting perpendicular to its plane. Obtain the expression for the torque acting on it.

Answer:

Consider a rectangular conducting loop (PQRS) of length l and b breadth b placed in a uniform magnetic field. Let I be the current flowing in the loop in a clockwise direction. Let at any instant the angle between the magnetic field and normal to the rectangular coil is θ.

Force acting on the ann PQ in the loop,

⇒ \(\overrightarrow{\mathrm{F}}_1=\mathrm{I}(\vec{\ell} \times \overrightarrow{\mathrm{B}}) \Rightarrow \mathrm{F}_1=\mathrm{IB} \ell\) (Directed inside the sheet of paper)

Similarly, the force acting on the arm RS of the loop,

⇒ \(\overrightarrow{\mathrm{F}}_2=\mathrm{I}(\vec{\ell} \times \overrightarrow{\mathrm{B}}) \Rightarrow \mathrm{F}_2=\mathrm{IB} \ell\) (Directed outside the sheet of paper)

Force \(\overrightarrow{\mathrm{F}}_3\) acting on the arm QR and force \(\overrightarrow{\mathrm{F}}_4\) acting on the arm SP of the loop are equal, opposite and act along the same line, hence they cancel each other. Therefore only two forces \(\overrightarrow{\mathrm{F}}_1\) and \(\overrightarrow{\mathrm{F}}_2\) act on the loop. \(\) and form a couple and try to rotate the loop clockwise. The magnitude of the torque(τ) due to forces \(\overrightarrow{\mathrm{F}}_1\) and \(\overrightarrow{\mathrm{F}}_2\) is given by

τ = Magnitude ol the either force x Perpendicular distance between forces

τ = IlB x b sin θ { l x b = A, area of the loop}

r = I A B sinθ

In vector form \(\vec{\tau}=I(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}})\)

If the loop has N turns, then the net torque acting on the loop is

τ = BINA sinθ

τ = M B sinθ

∴ \(\vec{\tau}=\overrightarrow{\mathrm{M}} \times \overrightarrow{\mathrm{B}}\)

CBSE Class 12 Physics Chapter 4 Question 9. How is a galvanometer converted into a voltmeter and an ammeter? Draw the relevant diagrams and find the resistance of the arrangement in each case. Take the resistance of the galvanometer as G.

Answer:

Conversion of Galvanometer into Voltmeter:

Voltmeter is used to measure p.d. so it is connected in parallel, in a circuit and its resistance should be infinite in the ideal case, thus to maximize the resistance of the galvanometer according to the required range we connect a suitable resistance in series as shown:

If the potential difference between the points to be measured = V and if

the galvanometer gives full-scale deflection when current “Ig” passes through it. Then.

⇒ \(V=I_g\left(R_g+R_X\right) \Rightarrow V=I_g R_g+I_g R_X \Rightarrow V-I_g R_g=I_g R_X\)

⇒ \(R_X=\left(V-I_g R_g\right) / I_g\)

⇒ \(R_x=\frac{V}{I_g}-R_g\)

Also, the equivalent resistance of the voltmeter: R_v = R_x + R_g

Conversion of Galvanometer into Anrmeter:

An ammeter is a current measuring device so its resistance should be zero in the ideal case, thus to minimize its resistance according to the required range, we connect a suitable resistance in parallel with it, which is called a shunt: \(I_S=\left(I-I_g\right)\)

The potential difference across the shunt: \(V_g=I_g R_g\)

But \(V_S=\left(I-I_g\right) R_S\)

V_s = V_g [in parallel combination]

⇒  \(\mathrm{R}_{\mathrm{S}}\left(\mathrm{I}-\mathrm{I}_{\mathrm{g}}\right)=\mathrm{I}_{\mathrm{g}} \mathrm{R}_{\mathrm{g}}\)

⇒ \(R_S=\frac{I_g}{I-I_g} R_g\)

Thus equivalent resistance \(G^{\prime}=\frac{R_g \cdot R_S}{R_g+R_S}\)

Question 10.

1. State Biot – Savart law and express this law in the vector form.
2. Two identical circular coils, P and Q each of radius R. carrying currents I A and √3A respectively, are placed concentric and perpendicular to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the center of the coils.

Answer:

1. Biot-Savart Law (BSL)

According to the Biot Savart Law, the magnitude of a magnetic field \(\mathrm{d} \overrightarrow{\mathrm{B}}\) is proportional to the current I. the element length \(\overrightarrow{\mathrm{dl}}\) and inversely proportional to the square of the distance r. Its direction is perpendicular to the plane containing \(\overrightarrow{\mathrm{dl}}\) and \(\overrightarrow{\mathrm{r}}\).

The field at point P due to the current element

⇒ \(\mathrm{dB}=\frac{\mu_0}{4 \pi} \frac{\mathrm{Id} \ell \sin \theta}{\mathrm{r}^2}\)

⇒ \(\frac{\mu_0}{4 \pi}=10^{-7} \mathrm{Tm} / \mathrm{A}\)

μ₀= permeability of free space (air/vacuum)

Vector form:

2.

Given

I₁ = I A (current in coil P) : I₂ = √3 A (current in coil Q)

The magnetic field at the center of the circular current-carrying coil is given by

B = μ₀ I/2R

So, \(B_p=\frac{\mu_0 I}{2 R}=\frac{\mu_0}{2 R}\)

∴ \(\mathrm{B}_{\mathrm{Q}}=\frac{\sqrt{3} \mu_0}{2 \mathrm{R}}\)

net field at centre(B_R)

⇒ \(B_R=\sqrt{B_p^2+B_Q^2}=\sqrt{\left(\frac{\mu_0}{2 R}\right)^2+\left(\frac{\sqrt{3} \mu_0}{2 R}\right)^2}\)

So, \(B_R=\frac{\mu_0}{R}\), Direction \(\tan \theta=\frac{\mathrm{B}_{\mathrm{p}}}{\mathrm{B}_{\mathrm{Q}}}=\frac{1}{\sqrt{3}}\)

θ = 30°

Question 11.

1. State Ampere’s circuital law.
2. Use this law to find the magnetic field due to a straight infinite current-carrying wire.
3. How are the magnetic field lines different from the electrostatic field lines?

Answer:

1. Ampere’s circuital law: The line integral of the magnetic field over a closed loop is p0 times the total current threading through that loop

⇒ \(\oint \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \vec{l}=\mu_0(\Sigma \mathrm{I})\)

2. Magnetic field due to infinitely long straight current carrying conductor:

Apply Ampere’s law to find out the magnetic field at point ’p’

⇒ \(\oint \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \vec{l}=\mu_0 \Sigma \mathrm{I}\)

⇒ \(\oint \mathrm{Bd} l \cos \theta=\mu_0 \mathrm{I} \quad\left\{\begin{array}{c}
\theta=0^{\circ} \\
\cos \theta=1 \\
\Sigma \mathrm{I}=\mathrm{I}
\end{array}\right.\)

⇒ \(\mathrm{B} \oint \mathrm{d} l=\mu_0 \mathrm{I} \Rightarrow \mathrm{B} \times 2 \pi \mathrm{r}=\mu_0 \mathrm{I}\)

⇒ \(B=\frac{\mu_0 I}{2 \pi r}\)

3. The magnetic field lines form continuous closed loops, whereas electrostatic field lines never form closed loops.

Question 12.

1. A point charge q moving with speed v enters a uniform magnetic field B that is acting into the plane of the paper as shown. What is the path followed by the charge q and in which plane does it move?
2. How does the path followed by the charge get affected if its velocity has a component parallel to \(\vec{B}\)?
3. If an electric field \(\vec{E}\) is also applied such that the particle continues moving along the original straight-line path, what should be the magnitude and direction of the electric field \(\vec{E}\)?

Answer:

1. Charge q moves in a circular path. It does move in X-Y plane.

2. If velocity has a component parallel to B then charge q moves in helical path.

3. \(\overrightarrow{\mathrm{V}}=-\mathrm{V} \hat{\mathrm{i}}\)

[∵ The particle is moving along negative x-direction]

⇒ \(\vec{B}=-B \hat{k}\)

∵ The magnetic field is perpendicular to the plane of the paper directed inwards i.e. negative z-direction.

∴ Force acting due to magnetic field \(F_m=q(\vec{v} \times \vec{B})=q[-v \hat{i} \times(-B \hat{k})]\)

∴ \(\overrightarrow{\mathrm{F}}_{\mathrm{m}}=-q v B \hat{\mathrm{j}}\) (∵ \(\hat{i} \times \hat{k}=-\hat{j}\))

The magnitude of F_m = qvB, in -Y direction

For the undeflected motion of particles.

Fe = qE should be applied in \(y(+\hat{j})\) direction.

CBSE Class 12 Physics Chapter 4 Moving Charges And Magnetism Long Questions And Answers

Question 1. Amperes law gives a method to calculate the magnetic field due to a given current distribution. According to it, the circulation \(\oint \vec{B} \cdot d \vec{l}\) of the resultant magnetic field along a closed boundary is equal to p0 times the total current crossing the area bounded by the closed curve provided the electric field inside the loop remains constant. Ampere’s law is more useful under certain symmetrical conditions. Consider one such case of a long straight wire with a circular cross-section (radius R) carrying current 1 uniformly distributed across this cross-section.

(1). The magnetic field at a radial distance r from the center of the wire in the region r > R, is

1. \(\frac{\mu_0 I}{2 \pi r}\)
2. \(\frac{\mu_0 I}{2 \pi R}\)
3. \(\frac{\mu_0 \mathrm{IR}^2}{2 \pi \mathrm{r}}\)
4. \(\frac{\mu_0 \mathrm{Ir}^2}{2 \pi \mathrm{R}}\)

Answer: 1. \(\frac{\mu_0 I}{2 \pi r}\)

(2). A long straight wire of a circular cross-section (radius a) carries a steady current I and the current I is uniformly distributed across this cross-section. Which of the following plots represents the variation of the magnitude of magnetic field B with distance r from the center of the wire?

Answer: 1.

(3). A long straight wire of radius R carries a steady current I. The current is uniformly distributed across its cross-section. The ratio of magnetic field al R/2 and 2R is

1. 1/2
2. 2
3. 1/4
4. 1

Answer: 4. 1

(4). A long straight wire of a very very thin radius carries a steady current I. How magnetic field at a distance from this wire change if the value of the current in the wire is doubled?

1. Doubled
2. Halved
3. Three times
4. None of the above

Answer: 1. Boubled

Question 2. Read the case study carefully and answer the questions that follow:

A galvanometer is a device used to detect current in an electric circuit. It cannot as such be used as an ammeter to measure current in a given circuit. This is because a galvanometer is a very sensitive device, It gives a full-scale deflection for a current of the order of μA.

Moreover, for measuring currents, the galvanometer has to be connected in series, and it has a large resistance, this will change the value of the current in the circuit. To overcome these difficulties, we connect a small resistance Rs, called shunt resistance, in parallel with the galvanometer coil, so that most of the current passes through the shunt.

Now to use a galvanometer as a voltmeter, it has to be connected in parallel with the circuit element across which we need to measure p.d. Moreover, it must draw a very small current, otherwise, it will appreciably change the voltage that we are measuring. To ensure this a large resistance R is connected in series with the galvanometer.

Based on the information given above, answer the following questions:

(1). A sensitive galvanometer like a moving coil galvanometer can be converted into an ammeter or a voltmeter by connecting a proper resistance to it. Which of the following statements is true:-

1. A voltmeter is connected in parallel and current through it is negligible
2. An ammeter is connected in parallel and the potential difference across it is small
3. A voltmeter is connected in series and the potential difference across it is small
4. An ammeter is connected in series in a circuit and the current through it is negligible

Answer: 1. A voltmeter is connected in parallel and current through it is negligible

(2). By mistake a voltmeter is connected in series and an ammeter is connected in parallel with a resistance in an electrical circuit. What will happen to the instruments?

1. Voltmeter is damaged
2. Ammeter is damaged
3. Both are damaged
4. None is damaged.

Answer: 4. None is damaged.

(3). A galvanometer coil has a resistance of 15 Ω and gives full-scale deflection for a current of 4 mA. To convert it to an ammeter of range 0 to 6 A.

1. 10 m Ω resistance is connected in parallel to the galvanometer.
2. 10 m Ω resistance is to be connected in series with the galvanometer.
3. 0.1 Ω resistance is to be connected in parallel to the galvanometer.
4. 0.1 Ω resistance is to be connected in series with the galvanometer.

Answer: 1. 10 m Ω resistance is connected in parallel to the galvanometer.

(4). A long straight wire of a very very thin radius carries a steady current I. How magnetic field at a distance from this wire change if the value of the current in the wire is doubled?

1. More
2. Equal
3. Less
4. Zero

Answer: 1. More

Question 3.

1. An α-particle, a deuteron, and a proton enter into a uniform magnetic field normally with the same kinetic energy and describe circular paths. Find the ratio of radii of their paths.

2. Give the direction of the magnetic field acting on the current-carrying coil ACDE shown in the figure so that the coil is in unstable equilibrium.

3. Why do we use a low resistance ammeter in a circuit to measure current?

Answer:

⇒ \(K=\frac{q^2 B^2 r^2}{2 m}\)

⇒ \(r=\sqrt{\frac{2 m K}{q^2 B^2}}\)

⇒ \(r=\frac{\sqrt{2 m K}}{q B}\)

K.B.2 → constant

⇒ \(r \propto \frac{\sqrt{m}}{q}\)

⇒ \(\begin{array}{c|c|c}
\alpha \rightarrow{ }_2 \mathrm{He}^{4} & \mathrm{d} \rightarrow{ }_1 \mathrm{H}^2 & \mathrm{P} \rightarrow{ }_1 \mathrm{H}^{1} \\
\mathrm{m}^{\prime}=4 \mathrm{~m} & \mathrm{~m}^{\prime \prime}=2 \mathrm{~m} & \mathrm{~m}=\mathrm{m} \\
\mathrm{q}^{\prime}=2 \mathrm{q} & \mathrm{q}^{\prime \prime}=\mathrm{q} & \mathrm{q}=\mathrm{q}
\end{array}\)

So, \(r_\alpha: r_d: r_p=\frac{\sqrt{4 m}}{2 q}: \frac{\sqrt{2 m}}{q}: \frac{\sqrt{m}}{q}\)

1:2:1

2. For an unstable equilibrium direction of the area and magnetic field must be opposite so the magnetic field must be in the Z direction.

3. So that maximum current flows through the ammeter.

Question 4.

1. Draw the magnetic field lines due to a circular wire carrying current I.
2. A square loop of sides 5 cm carrying a current of 0.2 A in the clockwise direction is placed at a distance of 10 cm from an infinitely long wire carrying a current of I A as shown. Calculate
   1. The resultant magnetic force, and
   2. The torque, if any, acting on the loop

Answer:

1. Magnetic field due to a circular wire carrying current I.

2. (1). Force on the side be an ad are same in magnitude and opposite in direction. So they cancel each other.

⇒ \(\overrightarrow{\mathrm{F}}_2=-\overrightarrow{\mathrm{F}}_4\)

⇒ \({\vec{F}}_2+\overrightarrow{\mathrm{F}}_{+}=0\)

Force on side (ab)

⇒ \(F_1=\left(\frac{\mu_0 I_1 I_2}{2 \pi d_1}\right) \times l\)

⇒ \(F_1=\left(\frac{4 \pi \times 10^{-7} \times 1 \times 0.2}{2 \pi \times 10}\right) \times 5\)

⇒ \(\mathrm{F}_1=2 \times 10^{-8} \mathrm{~N}\) (towards left)

Force on side (cd)

⇒ \(\mathrm{F}_3=\left(\frac{\mu_0 \mathrm{I}_1 \mathrm{I}_2}{2 \pi \mathrm{d}_2}\right) \times l\)

⇒ \(F_3=\left(\frac{4 \pi \times 10^{-7} \times 1 \times 0.2}{2 \pi \times 15}\right) \times 5 \Rightarrow F_3=\frac{4}{3} \times 10^{-8} \mathrm{~N}\)

The resultant force on the loop,

F = F₁-F₂ (∵ F₁ and F₃ are oop.)

\(\)\left(2-\frac{4}{3}\right) \times 10^{-8} \Rightarrow \mathrm{F}=\frac{2}{3} \times 10^{-8} \mathrm{~N} (towards left)

(2). Torque on square loop ‘Abcd’

τ = MB sinθ (∵ θ = 0)

τ = 0

Question 5.

1. With the help of a neat and labeled diagram, explain the principle and working of a moving coil galvanometer.
2. What is the function of a uniform radial field and how it is produced?
3. Define the current sensitivity of a galvanometer. How is current sensitivity increased?

Answer:

1. Principle: When the current-carrying coil is placed in a magnetic field it experiences a torque.

τ = NI AB → (1)

It consists of a plane coil of many turns suspended in a radial magnetic field. When a current is passed in the coil it experiences a torque which produces a twist in the
suspension.

This deflection is directly proportional to the torque

τ= KΦ → (2)

By equation (1) and (2)

∵ N1AB = KΦ;

⇒ \(I=\left(\frac{K}{N A B}\right) \phi\);

K = elastic torsional constant of the suspension

⇒ \(\mathrm{I}=\mathrm{C} \phi ; \mathrm{C}=\frac{\mathrm{K}}{\mathrm{NAB}}\)

C ⇒ Galvanometer constant

So I ∝ Φ

τ ∝ I

Galvanometer:

An instrument used to measure the strength of current by measuring the deflection of the coil due to torque produced by a magnetic field.

τ ∝ i∝θ

Current Sensitivity (CS)

It is defined as the deflection per unit current.

⇒ \(C S=0 / I=\frac{N A B}{K}\)

Voltage Sensitivity (VS)

It is defined as deflection per unit voltage.

⇒ \(V S=\phi / V=Φ / I R=\left(\frac{N A B}{K R}\right)\)

2. The function of radial field, is.

1. To maximize the deflecting torque acting on the current carrying coil.
2. To increase the strength of the magnetic field.

The radial magnetic field is produced by using a concave magnetic pole. Also cylindrical soft iron core helps in the production of the radial magnetic field.

3. Current sensitivity is the deflection shown by the galvanometer for a unit current flow.

⇒ \(I_S=\frac{\phi}{I} \text { or } \frac{N A B}{K}\)

Where Φ is the deflection in the coil.

The current sensitivity of the galvanometer can be increased by

1. Increasing the number of turns (N )
2. Increasing magnetic induction (B)
3. Increasing area of coil (A)
4. Decreasing the couple per unit twist of the spiral springs.

Question 6.

1. Use it to obtain the expression for the magnetic field at an axial point situated at distance d from the center of a circular coil of radius R carrying current I.
2. Also, find the ratio of the magnitudes of the magnetic field of this coil at the center and at an axial point for which x = R√3.

Answer:

1. Vector form of Biot-Savart’s law

⇒ \(d \vec{B}=\frac{\mu_0 I}{4 \pi r^2}(d \vec{l} \times \hat{r})\left\{\hat{r}=\frac{\vec{r}}{r}\right.\)

The magnetic field at an axial point of a current-carrying circular loop:

⇒ \(d\vec{B}=\frac{\mu_{0} \mathrm{I}}{4 \pi \mathrm{r}^3}(\mathrm{~d} \vec{l} \times \overrightarrow{\mathrm{r}})\)

Magnetic field due to the small element at point ‘P’

⇒ \(\mathrm{dB}=\frac{\mu_0 \mathrm{Id} l \sin \theta}{4 \pi r^2}\)

Angle between \(d\vec{l}\) and \(\hat{r}\) is always 90 ( = 90°). The direction of the magnetic field is perpendicular to the plane of \(d\vec{l}\) and \(\hat{r}\).

⇒ \(\mathrm{dB}=\frac{\mu_0 \mathrm{Id} l}{4 \pi \mathrm{r}^2}\left\{\sin 90^{\circ}=1\right.\)

The total magnetic field at point P

⇒ \(\mathrm{B}_{\text {axis }}=\int_0^{2 \pi \mathrm{R}} \mathrm{dB} \sin \phi\) ⇒ \(\mathrm{B}_{\mathrm{axis}}=\int_0^{2 \pi \mathrm{R}} \frac{\mu_0 \mathrm{Id} l}{4 \pi \mathrm{r}^2} \times \frac{\mathrm{R}}{\mathrm{r}}\left\{\sin \phi=\frac{\mathrm{R}}{\mathrm{r}}\right.\)

⇒ \(\mathrm{B}_{\mathrm{axis}}=\frac{\mu_0 \mathrm{IR}}{4 \pi \mathrm{r}^3} \int_0^{2 \pi \mathrm{R}} \mathrm{d} l\) ⇒ \(B_{\text {axis }}=\frac{\mu_0 I R}{4 \pi r^3} \times 2 \pi R\) ⇒ \(\mathrm{B}_{\mathrm{axis}}=\frac{\mu_0 \mathrm{IR}^2}{2 \mathrm{r}^3}\)

⇒ \(B_{\mathrm{axis}}=\frac{\mu_0 I R^2}{2\left(R^2+x^2\right)^{3 / 2}}\left\{r=\left(R^2+x^2\right)^{1 / 2}\right.\)

⇒ \(B_{\text {axis }}=\frac{\mu_0 \text { NIR }^2}{2\left(R^2+x^2\right)^{3 / 2}}\)

2. At the center of the current loop

⇒ \(B_0=\frac{\mu_0 N I}{2 R}\)

At the axial point x = R√3

⇒₁\(B_1=\frac{\mu_0 NI R^2}{2\left(R^2+3 R^2\right)^{3 / 2}}=\frac{\mu_0 NI R^2}{2 \times 8 R^3}\)

⇒ \(\frac{B_0}{B_1}=\frac{\frac{\mu_0 N I}{2 R}}{\frac{\mu_0 N I}{2 \times 8 R}}=8: 1\)