Relations and Functions Class 12 Maths Important Questions Chapter 1

Relations And Functions Exercise 1.1

Question 1. Determine whether each of the following relations is reflexive, symmetric, or transitive :

1.  Relation R in the set A = {1,2, 3…13, 14} defined as R = {(x, y): 3x – y = 0}
2.  Relation R in the set N of natural numbers defined as R = {(x, y): y = x + 5 and x < 4}
3. Relation R in the set A = (1, 2, 3, 4, 5, 6} as R = {(x, y); y is divisible by x}
4.  Relation R in the set Z of all integers defined as R = {(x, y): x – y is an integer}
5.  Relation R in the set A of human beings in a town at a particular time given by
   1.  R = {(x, y): x and y work at the same place}
   2. R = {(x, y): x and y live in the same locality}
   3.  R – {(x, y): x is exactly 7 cm taller than y}
   4.  R = {(x, y): x is wife of y)
   5.  R = {(x, y): x is father of y}

Solution:

1. A = {1,2, 3 … 13, 14}; R = {(x, y): 3x -y = 0}

Reflexive: R = {(1, 3), (2, 6), (3, 9), (4, 12)}

(1,1) ∉ R, So, R is not reflexive.

Symmetric: (1, 3) ∈ R, but (3, 1) ∉ R. So, R is not symmetric

Transitive: (1,3), (3, 9) ∈ R, but (1, 9) ∉ R. So, R is not transitive

Hence, R is neither reflexive, nor symmetric, nor transitive.

2. R = {(x, y): y = x + 5 and x < 4} ⇒ R ~ {(1, 6), (2, 7), (3, 8)}

Reflexive:  (1, 1) ∉ R. So, R is not reflexive.

Symmetric : (1,6) ∈ R, but (6, 1) ∉ R. R is not symmetric.

Transitive: Since there are no three elements x, y, z ∈ N such that (x, y) ∈ R, z) ∈ R but (x, z) ∉ R

∴ R is transitive. Hence, R is neither reflexive nor symmetric but it is transitive.

3. A = {1, 2, 3,4, 5, 6}; R = {(x, y): y is divisible by x}

Reflexive: Let x∈ A such that if (x, x) ∈ R x is divisible by x, which is true, ∀ x∈ A

∴ R is reflexive.

Read and Learn More Class 12 Maths Chapter Wise with Solutions

Symmetric: Let x, y ∈ A such that if (x, y) ∈ R => y is divisible by x

⇒ x is not divisible by => (y, x) ∉R

For example: (2, 4) ∈ R but (4, 2) ∉R.

∴ R is not symmetric.

Transitive: Let x, y, z ∈ A such that if (x, y) ∈ R and (y, z) ∈ R

⇒ y is divisible by x and z is divisible by y.

⇒ \(\frac{y}{x}=k_1 \in I \)  → Equation 1

⇒ \((y, z) \in R \Rightarrow \frac{z}{y}=k_2 \in\) I  → Equation 2

Equation (1) x (2) gives

⇒ \(\frac{y}{x} \times \frac{z}{y}=k_1 \times k_2 \Rightarrow \frac{z}{x}=\left(k_1 k_2\right) \in\) I

(x, z)\( \in\)

∴ R . R is transitive.

Hence, R is reflexive and transitive but not symmetric.

(4) R = {(x, y): x – y is an integer}

Reflexive: If (x, x) ∈R ⇒ x – x = 0, which is an integer, ∀ x ∈ Z.

∴ R is reflexive.

Symmetric: If (x, y) ∈ R ⇒ (x – y) is an integer. ⇒ (y – x) is also an integer.

⇒ (v. x) ∈R

∴ R is symmetric.

Transitive: If (x, y) ∉ R ⇒ x -y = k₁ ∈  (1)

and (y, z) ∈ R ⇒ y – z = k₂ ∈  (2)

Adding equation (1) and (2), we get

(x – y) + (y – z) = (k₁ + k₂) ∈

x – z = (k₁ + k₂) ∈ I

⇒ (x, z) ∈ R

∴ R is transitive.

Hence, R is reflexive, symmetric, and transitive.

5. Given A = (x : x is a human being in a town}

(1.) R = {(x, y): x and y work at the same place}

Reflexive: If (x, x) e R ⇒ x and x work at the same place, which is true, V x ∈ A R is reflexive.

Symmetric: If (x, y) ∈ R ⇒ x and y work at the same place.

⇒ y and x also work at the same place. ⇒ (y, x)∈R.

∴R is symmetric.

Transitive: If (x, y) ∈ R and (y, z) ∈ R

⇒ x and y work at the same place and y and z work at the same place.

⇒ x and z work at the same place. ⇒ (x, z) ∈ R

∴ R is transitive.

Hence, R is reflexive, symmetric, and transitive.

(2) R = {(x, y): x and y live in the same locality}

Reflexive: If (x, x) e R => x and x live in the same locality, which is true, ∀ x ∈ A

∴ R is reflexive.

Symmetric: If (x, y) ∈ R ⇒ x and y live in the same locality.

⇒ y and x also live in the same locality ⇒ (y, x) ∈ R

∴ R is symmetric.

Transitive: Let (x, y) ∈ R and (y, z) ∈ R.

x and y live in the same locality and y and z live in the same locality.

⇒ x and z live in the same locality. ⇒ (x, z) ∈ R

R is transitive. Hence, R is reflexive, symmetric, and transitive.

(3.) R = {(x, y): x is exactly 7 cm taller than y}

Reflexive: If (x, x) ∈ R ⇒ x is exactly 7 cm taller than x, which is not true, for any x ∈ A. Since human beings x cannot be taller than themselves.

∴ So, R is not reflexive.

Symmetric: If (x, y) ∈ R ⇒ x is exactly 7 cm taller than y ⇒ y is exactly 7 cm smaller

⇒ (y, x)∉ R

∴ R is not symmetric.

Transitive: If (x, y), (y, z) ∈ R

⇒ x is exactly 7 cm taller than y and y is exactly 7 cm taller than z.

⇒ x is exactly 14 cm taller than z.

∴ (x, z) ∉ R

∴ R is not transitive.

Hence, R is neither reflexive, nor symmetric, nor transitive.

(4) R = ((x, y): x is wife of y)

Reflexive: If (x, x) ∈ R ⇒ x is wife of x, which is not true, for any x ∈ A

∴ R is not reflexive.

Symmetric; If (x, y) ∈ R ⇒ x is the wife of y ⇒ y is the husband of x.

(y, x) ∉ R

R is not symmetric.

Transitive: There are no three elements x, y, z ∈ A such that (x, y) R and (y, z) ∈ R but (x, z) ∉ R

So, R is transitive. Hence, R is neither reflexive, nor symmetric, but R is transitive.

(5) R = {(x, y): x is father of y}

Reflexive: If (x, x) ∈ R ⇒ x is the father of x, which, is not true, for any x ∈ A

∴ R is not reflexive.

Symmetric: If (x, y) ∈ R ⇒ x is the father of y ⇒ his son or daughter of x.

(y,x) ∉ R R is not symmetric.

Transitive: If (x, y) ∈ R and (y, z) ∈ R,

x is the father of y, and y is the father of z ⇒ x is the grandfather of z.

(x, z) ∉ R

R is not transitive. Hence, R is neither reflexive, symmetric, nor transitive.

Question 2. Show that the relation R in the set R of real numbers, defined as R = {(a, b): a < b} is neither reflexive nor symmetric nor transitive.

Solution:

Reflexive: R = {(a, b): a \(\leq b^2\)}

Let a ∈ R such that if (a, a) ∈ R ⇒ a ≤ a² is not true for all a ∈ R

i.e. (a, a) \(\notin R, \forall a \in\) R

Let a=\(\frac{1}{2} \in\) R

⇒ \(\frac{1}{2}\) ≰  \(\frac{1}{2^2}\) ⇒ \(\frac{1}{2}\) ≰  \(\frac{1}{4}\) ∈ R

∴ R is Not Reflexive

Symmetric: Let a, b ∈ R such that if (a, b) ∈ R ⇒ a ≤ b² ⇒ b≰  a²

For example. 2≰ 5² ⇒(2,5) ∈ R but 5≰ 2²

⇒ (5,2) ∉ R

∴ R is not symmetric

Transitive: Let a,b,csR such that if (a, b) ∈ R an nd (b. c) ∈ R

⇒ a ≤ b² and b ≤ c² ⇒ a ≰ c²

For Example: 5 ≤ 3²  and 3 ≤ 2² but 5 ≰ 2²

(5, 3) e R and (3, 2) ∈ R but (5, 2) ∉R

∴ R is not transitive

∴ Hence, R is neither reflexive nor symmetric nor transitive.

Question 3. Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b): b = a + 1} is reflexive, symmetric, or transitive.

Solution:

Reflexive: Given A = {1, 2, 3, 4, 5, 6}.

R = {(a, b): b = a + 1} ⇒ R = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)} v (1,1) ∉ R, where 1 ∈ A

∴ R is not reflexive.

Symmetric: (1, 2) 6 R but (2, 1) ∉ R, where 1, 2 ∉ A.

∴ So R is not symmetric

Transitive: (1, 2) ∈ R and (2, 3) ∈ R but (1, 3) ∉ R, where 1,2,3 ∈ A.

R is not transitive Hence R is neither reflexive, symmetric, nor transitive.

Question 4. Show that the relation R in R defined as R = {(a, b): a < b}, is reflexive and transitive but not symmetric.

Solution:

Reflexive: Given R = {(a, b): a < b}

Let a ∈ R such that if (a, a) ∈ R ⇒ a < a, which is true, ∀a∈R

∴ R is reflexive

Symmetric: Let a, b e R such that if (a, b) e R ⇒ a < b ⇒ b > a ⇒ (b, a) ∉ R

For example: 1 < 2 ⇒ (1, 2) e R But 2 ∉1 ⇒ (2,1)

∴ R is not symmetric

Transitive: Let a, b, c ∈ R such that if (a, b) ∈ R and (b, c) ∈ R ⇒ a < b and b<c ⇒ a<c ⇒ (a, c) ∈ R

∴ R is transitive

Flence R is reflexive and transitive but not symmetric.

Question 5. Check whether the relation R in R defined as R = {(a, b): a < b³} is reflexive, symmetric, or transitive.

Solution:

Reflexive: Given R = {(a, b): a < b³}

Let a∈ R such that if (a, a) ∈ R ⇒ a < a’

Not true for all a ∈ R ⇒ (a, ) R, ∀ a ∈ R 1

Let a = \(\frac{1}{2} \in \mathrm{R}\)

⇒ \(\frac{1}{2} \notin \frac{1}{2^3} \Rightarrow \frac{1}{2} \notin \frac{1}{8} \Rightarrow\left(\frac{1}{2}, \frac{1}{2}\right) \notin \mathrm{R}\)

∴ R is not Reflexive.

Symmetric: Let a, b ∈ R such that if (a, b) ∈ R ⇒ a < b³ ⇒ b∉ a³

For example: 2 < 9J but ∈ ∉ 21 => (2, 9)∈R but (9, 2) ∉ R

∴ R is not symmetric

Transitiv e: Let a, b, c ∈ R such that if (a, b) ∈ R and (b, c) ∈ R

⇒ a < b³ and b < c³ ⇒ a ∉ c³

For example: 9 < 33 and 3 < 2 but 9

⇒ (9,3) ∈ R and (3,2) ∈ R but (9,2) ∉ R

∴ R is not transitive

∴ Hence R is neither reflexive nor symmetric nor transitive.

Question 6. Show that the relation R in the set {1,2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.

Solution:

Reflexive: Let A = {1, 2, 3}.

A relation R on A is defined as R = {(1, 2), (2,1)}.

v (1,1) ∉ R, where 1 ∈ A R is not reflexive

Symmetric: (1,2) ∈ R and (2,1) ∈ R

∴ R is symmetric

Transitive: (1,2) ∈ R and (2,1) ∈ R but (1,1) ∉ R

∴ R is not transitive

Hence, R is symmetric but neither reflexive nor transitive.

Question 7. Show that the relation R in the set A of all the books in a library of a college, given by R = {(x, y): x and y have same number of pages} is an equivalence relation.

Solution:

Reflexive: Set A is the set of all books in the library of a college. R = {(x, y): x and y have the same number of pages}

Let x ∉ A such that if (x, x) ∈ R ⇒ x and x have the same number of pages.

Which is the true, V x ∈ A

∴R is reflexive

Symmetric: Let x, y ∈ A such that if (x, y) ∈ R ⇒ x and y have the same number of pages.

⇒ y and x have the same number of pages. ⇒ (y, x)∈ R

∴ R is symmetric.

Transitive: Let x, y, z ∈ A such that if (x, y) ⇒ R and (y, z)∈ R.

⇒ x and y have the same number of pages and y and z have the same number of pages.

⇒ x and z have the same number of pages ⇒ (x, z) ∈ R

∴ R is transitive.

Since, R is reflexive, symmetric, and transitive on A

∴ Hence, R is an equivalence relation to A.

Question 8. Show that the relation R in the set A = {1, 2, 3, 4, 5} given by R = {(a, b): |a – b| is even}, is an equivalence relation. Show that all the elements of {1,3, 5} are related to each other and all the elements of {2, 4} are related to each other. But no element of {1, 3, 5} is related to any element of {2,4}.

Solution:

Reflexive: A = {1,2,3,4, 5}, R = [{a, b);| a — b| is even}

Let a ∈ A such that if (a, a) ∈ R ⇒ |a – a| = 0, is even

which is true, ∀ a ∈ A

∴ R is reflexive.

Symmetric: Let a, b ∈ A such that if (a, b) ∈ R ⇒ |a- b| is even |-(b – a)| = |b – a| is also even

⇒ (b, a) ∈ R

∴ R is symmetric.

Transitive: Let a, b, c ∈ R such that if (a, b) ∉ R and (b, c) ∈ It

⇒ |a — b| and |b – c| both are even

⇒ |a-b| = 2k, and | b — c| = 2k₂, (k₁,k₂ ∈ Z)

⇒  (a-b) = ±2k,(1) and (b-c) = ± 2 k₂  (2)

On adding equations (1) & (2), we get:

(a-c) = ± 2(k₁+ k₂) ⇒ |a-c| = 2(k₁ + k₂)

⇒ |a – c| is even ⇒ (a, c) ∈ R (v k₁ + k₂ ∈ Z)

∴ R is transitive

Since R is reflexive, symmetric, and transitive on A.

Hence, R is an equivalence relation to A.

Since the difference of two even (or odd) is always even.

So, every element of set {1, 3, 5} is related to each other and also every element of set {2,4} is related to each other but no element of {1,3, 5} is related to any element of {2,4}.

Question 9. Show that each of the relation R in the set A = {x∈Z : 0 < x < 12), given by

1. R = {(a, b): |a — b| is a multiple of 4}

2. R = {(a, b): a = b} is an equivalence relation. Find the set of all elements related to 1 in each case.

Solution:

Given that: A = (x ∈ Z : 0 ^x <. 12} = {0, 1,2, 3,4, 5, 6,7, 8,9,10,11,12}

1. R = {(a, b): |a – b|} is a multiple of 4}

Reflexive: Let a ∈ A such that if (a, a) ∈ R ⇒ |a- a| = 0 is a multiple of 4 which is true,∀ a ∈ A

∴ R is reflexive.

Symmetric: Let a, b ∈ A such that if (a, b) ∉ R ⇒ |a – b| is a multiple of 4.

⇒ |b – a| is also a multiple of 4,

(b, a) ∈ R

∴ R is symmetric.

Transitive: Let a, b, c ∉ A such that if (a, b) ∈ R and (b, c) ∈ R

⇒ |a — b| and |b – c| both are multiple of 4

⇒ |a-b| = 4k₁ and |b-c| = 4k₂ (k₁ k₂ ∈ Z)

⇒ a-b = ±4k₁ (1) and b-c = ±4k₂ → (2)

On adding equations (1) & (2), we get:

a – c = ± 4 (k₁ + k₂) ⇒ |a-c| = 4(k₁ + k₂)

|a – c| is multiple of 4 (∴  k₁ + k₂ ∈ Z)

(a, c) ∈ R

∴ R is transitive

Since R is reflexive, symmetric, and transitive on A

Hence, R is an equivalence relation on A,

Further, let x ∈ A such that (x, 1) ∈ R

|x-1| is multiple of 4 ⇒ |x- 11 = 0,4, 8,

x-1 =0,4,8 ⇒ x- 1,5,9

Hence, required set ={1,5,9}

2. R= {(a, b): a = b}

Reflexive: Let a ∈A, such that (a, a) ∉ R, ⇒ a = a. which is true, ∀ a ∈ A.

∴ So, R is reflexive.

Symmetric: Let a, b ∉ A such that if (a, b) ∈ R.

⇒ a = b ⇒ b~a ⇒ (b, a) ∈ R

∴ R is symmetric.

Transitive: Let a, b, c ∈ A such that if (a, b) ∈ R and (b, c) ∈ R.

⇒ a = b and b = c a = c (a, c) ∈ R

∴  R is transitive.

Since R is reflexive, symmetric, and transitive on A

Hence, R is an equivalence relation on A

Let x ∈ A such that (x, 1) ∈ R ⇒ x  – 1

Hence, required set = {1}

Question 10. Give an example of a relation. Which is

1.  Symmetric but neither reflexive nor transitive.
2.  Transitive but neither reflexive nor symmetric,
3.  Reflexive and symmetric but not transitive.
4.  Reflexive and transitive but not symmetric.
5. Symmetric and transitive but not reflexive.

Solution:

(1) Let A = {5,6, 7}.

Reflexive: Define a relation R on A as R = {(5, 6), (6, 5)}.

Since (5,5) ∉ R, where 5 ∈ A.

∴ So, R is not reflexive

Symmetric: Since (5, 6) ∈ R and (6, 5) ∈ R. So, R is symmetric

Transitive: Since (5, 6) ∈ R and (6, 5) ∈ R but (5, 5) ∉ R.

So, R is not transitive Hence, relation R is symmetric but neither reflexive nor transitive.

2. Consider a relation R in N defined as:

R = {(a, b): a < b)

Reflexive: Let a ∈ N such that if (a, a) ∈ R ⇒ a < a, which is not true for any a ∈ N

∴  R is not reflexive

Symmetric: Let a, b e N such that if (a, b) ∈ R ⇒ a < b:⇒ b > a ⇒ (b, a) ∉ R

∴  R is not symmetric

Transitive: Let a, b, c ∈ N such that if (a, b) ∈ R and (b, c) ∈ R

a < b and b < c ⇒ a < c

(a, c) ∈ R.

∴ So, R is transitive

Hence, relation R is transitive but neither reflexive nor symmetric.

3. Let A = {4, 6, 8}.

Define a relation R on A as R = {(4, 4), (6, 6), (8, 8), (4, 6), (6, 4), (6, 8), (8, 6)}

Reflexive: Since, (a, a) ∈ R, ∀ a ∈ A.

∴ So, R is reflexive

Symmetric: Since, (a, b) ∉ R (b, a) ∈ R, for all a, b ∈ A.

∴ So, R is symmetric.

Transitive: Since, (4, 6) ∈ R and (6, 8) ∈ R but (4, 8) R.

∴ So, R is not transitive.

Hence, R is reflexive symmetric but not transitive.

4. Define a relation R, in R as: R, = {(a, b): a > b}

Reflexive: Let a ∈ R₁ such that if (a, a) ∉ R₁ ⇒ a³ > a, which is true ∀ a ∈ R

∴ R₁ is reflexive.

Symmetric: Let a, b e R₁ such that if (a, b) ∈ R₁ a³ ≥ b³ => b³≤ a³

For example: 2³≥ 1³ but 1³ ≤ 2³

(2, 1) ∈ R, but (1,2) ∉ R₁

∴ R₁ is not symmetric.

Transitive: Let a, b, c ∈ R such that if (a, b) ∉ R₁ and (b, c) ∈ R₁

⇒ a³≥ b³ and b³ ≥ c³ ⇒ a³≥ c³ ⇒ (a, c) ∈ R₁

∴ R is transitive.

Hence, relation R₁ is reflexive and transitive but not symmetric,

5. Let A = {1,2, 3}.

Define a relation R on A as: R = {(1, 1) (2, 2)}

Reflexive: Since (3, 3) ∉R, where 3 ∈ A. So, R is not reflexive

Symmetric: If (a, b) ∈ R

Here, a = b ⇒ b = a ⇒ (b, a)∈R

∴ R is symmetric

Transitive: If (a, b)∈R and (b,c)∈R Here a = b and b = c ⇒ a = c

(a, c) ∈ R

∴  R is transitive

Hence, relation R is symmetric and transitive but not reflexive.

Question 11. Show that the relation R in the set A of points in a plane given by R = {(P, Q): distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, shows that the set of all points related to a point P * (0, 0) is the circle passing through P with the origin as the center.

Solution:

Given the set A of points in a plane and a relation R on A selection as

R = {(P, Q): distance of point P from the origin is the same as the distance of point Q from the origin}

Reflexive: Let P ∈ A such that if (P, P) ∈ R ⇒ OP = OP, which is true, ∀P ∈ A

∴ R is reflexive.

Symmetric: Let P, Q ∈ A such that if (P, Q) ∈ R ⇒ OP = OQ ⇒ OQ = OP ⇒ (Q, P) ∈ R

∴ R is symmetric.

Transitive: Let P, Q, S ∈ A such that if (P, Q) ∈ R and (Q, S) ∈ R ⇒ OP = OQ and OQ = OS ⇒ OP = OS (P, S) ∈ R

∴ R is transitive.

Since R is reflexive symmetric and transitive.

Hence, R is an equivalence relation.

The set of all points related to P ≠ (0,0) will be those points whose distance from the origin is the same as the distance of point P from the origin.

In other words, If O (0, 0) is the origin and OP – k, then the set of all points related to P is at a distance of k from the origin.

Hence, this set of points forms a circle with the center as the origin and this circle passes through point P.

Question 12. Show that the relation R defined in the set A of all triangles as R = {(T₁ T₂): T₁ is similar to T₂}, is an equivalence relation. Consider three right angle triangles T₁ with sides 3, 4, 5, T₂ with sides 5,12,13, and T₃ with sides 6,8,10. Which triangles among T₁ T₂ and T₃ are related?

Solution:

Given, set A of all triangles and a relation R on A defined by R = {(T₁ T₂): T₁ is similar to T₂ Reflexive: Since every triangle is similar to itself,

∴ R is reflexive

Symmetric: Let T₁ T₂ ∈ A such that if (T₁ T₂) ∉ R ⇒ T, is similar to T₂ ⇒ T₂ is similar to T₁

⇒ (T₂T₁) ∈ R

∴ R is symmetric.

Transitive: Let T₁ T₂, T₃ ∈ A such that if (T₁ T₂), (T₂ T₃) ∈ R.

⇒ T₁ is similar to T₂ and T₂ is similar to T₃.

⇒ T₁ is similar to T₃. ⇒ (T₁ T₃) ∈ R

∴ R is transitive.

Since, R is reflexive, symmetric, and transitive.

Hence, R is an equivalence relation.

Given three right angle triangles T₁ with sides 3,4, 5, T₂ with sides 5,12,13 and T₃ with sides 6,8,10

\(\frac{3}{6}=\frac{4}{8}=\frac{5}{10}=\frac{1}{2}\)

Since the corresponding sides of triangles T₁ and T₃ are in the same ratio.

Then, triangle T₁ is similar to triangle T₃

Hence, T₁ is related to T₃

Question 13. Show that the relation R defined in the set A of all polygons as R = {(P₁ P₂): P₁ and P₂ have same number of sides}, is an equivalence relation. What is the set of all elements in A related to the right-angled triangle T with sides 3, 4, and 5?

Solution:

Given a relation R defined in the set A of all polygons as :

R = {(P₁ P₂): P₁ and P₂ have the same number of sides}

Reflexive: Let P, ∈ A such that if (P₁ P₂) ∈ R as the same polygon has the same number of sides with itself.

∴ R is reflexive.

Symmetric: Let P₁ P₂ ∈ A such that if (P₁ P₂) ∈ R ⇒ P₁ and P₂ have same number of sides

⇒ P₃ and P₁ have same number of sides ⇒ (P₂, P₁) ∈ R

∴ R is symmetric.

Transitive: Let P₁ P₂, P₃ ∈ A such that

If(P₁P₂), (P₂, P₃)∈R.

P₁ and P₃ have the same number of sides, and P₂ and P₃ have the same number of sides.

⇒ P₁ and P₃ have the same number of sides.

⇒ (P₁ P₃) ∈ R R is transitive.

Since R is reflexive, symmetric, and transitive Hence, R is an equivalence relation.

The elements in A related to the right-angled triangle (T) with sides 3, 4, and 5 are those polygons that have 3 sides (since T is a polygon with 3 sides).

Hence, the required set is the set of all triangles of A which are related to T.

Question 14. Let L be the set of all lines in XY plane and R be the relation in L defined as R = {(L₁ L₂): L₁ is parallel to L₂}. Show that R is an equivalence relation. Find the set of all lines related to the line y = 2x + 4.

Solution:

Given, L is the set of all lines in XY plane and relation R on set L defined as R = {(L₁ L₂): L₁ is parallel to L₂}

Reflexive: Let L₁ ∈ L such that if (L₁ L₂) ∈ R L₁ ||

L₁ which is true, ∀ L₁ ∈ L

∴ R is reflexive

Symmetric: Let L₁ L₂ ∈ L such that if (L₁ L₂) ∈ R.

⇒ L₁ is parallel to L₂ ⇒ L₂ is parallel to L₁ ⇒  (L₂, L₁) ∈ R

∴ R is symmetric.

Transitive: Let L₁ L₂ L₃ ∈ L such that if (L₁ L₂), (L₂, L₃) ∈ R.

L₁ is parallel to L₂ and L₂ is parallel to L₃

⇒ L₁ is parallel to L₃

∴ R is transitive.

Since R is reflexive, symmetric, and transitive

Hence, R is an equivalence relation.

The set of all lines related to the line y = 2x + 4 is the set of all lines that are parallel to the line y = 2x + 4.

The slope of line y = 2x + 4 is m = 2.

It is known that parallel lines have the same slope.

The line parallel to the given line is of the form y = 2x + ∈, where c ∈ R.

Hence, the set of all lines related to the given line Is given by y = 2x + c, where c ∈ R.

Question 15. Let R be the relation in the set {1, 2, 3, 4} given by R = {(1, 2), (2. 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}.

Choose the correct answer.

1. R is reflexive and symmetric but not transitive.
2. R is reflexive and transitive but not symmetric.
3. R is symmetric and transitive but not reflexive.
4. R is an equivalence relation,

Solution:

(B) Let A = {1,2, 3, 4}, given a relation R on A defined as R = {(1,2), (2, 2), (1, 1)( (4, 4), (1, 3), (3, 3), (3, 2)}

Reflexive: Since (a, a) ∈ R, ∀ a ∈ A.

∴ So, R is reflexive.

Symmetric: Since, (1,2) ∈ R, but (2, 1) ∉ R.

∴  So, R is not symmetric.

Transitive: Since at least three elements a, b, c ∈ A do not exist Such that (a, b)∈ R and (b, ∈) ∉ R ⇒ (a, c) ∉ R

∴ R is transitive.

Hence, R is reflexive and transitive but not symmetric.

Question 16. Let R be the relation in the set N given by R = {(a, b): a = b – 2, b > 6}. Choose the correct answer.

1. (2, 4) ∈ R
2. (3, 8) ∈ R
3. (6, 8) ∈ R
4.  (8, 7) ∈ R

Solution:  3.

R = {(a, b): a = b – 2, b > 6}

∴ b > 6 and a = b – 2

R = {(5, 7), (6, 8), (7, 9) }

Here (6, 8) ∈ R

Relations And Functions Exercise 1.2

Question 1. Show that the function f: \(\mathrm{R}_* \rightarrow \mathrm{R}_*\) defined by f(x) = \(\frac{1}{x}\) is one-one and onto, where \(\mathrm{R}_*\) is the set of all non-zero real numbers. Is the result true, if the domain \(\mathrm{R}_*\) is replaced by N with the co-domain being the same as \(\mathrm{R}_*\)?

Solution:

Given that f : \(\mathrm{R}_* \rightarrow \mathrm{R}_*\) is defined by f(x) = \(\frac{1}{x}\)

Let x₁ x₂ ∉ \(\mathrm{R}_*\) (domain) such that if f\(f\left(x_2\right) \Rightarrow \frac{1}{x_1}=\frac{1}{x_2} \Rightarrow x_1=x_2\)

∴ f is one-one.

y ∈ \(\mathrm{R}_*\) (codomain) and f(x) = y

⇒ \(\frac{1}{x}=y \Rightarrow x=\frac{1}{y} \forall y \in R, \text { there exists } x=\frac{1}{y} \in R \text { such that } f(x)=\frac{1}{\left(\frac{1}{y}\right)}\)=y

∴ f is onto.

Thus, the given function f is one-one and onto.

Now, consider function g : N →\(\mathrm{R}_*\) defined by g(x) = \(\frac{1}{x}\)

Let x₁ x₂ ∈ N

Let y∈\(\mathrm{R}_*\), and if g(x,) = \(\frac{1}{x_1}=\frac{1}{x_2} \Rightarrow x_1=x_2\)

∴ g is one-one.

Let y=g(x)=\(\frac{1}{x} \Rightarrow x=\frac{1}{y} \notin N, \forall y \in \mathrm{R}_*\)

For example: y=\(\frac{2}{3} \in \mathrm{R}_*\) then x=\(\frac{3}{2} \notin N\)

∴ g is not onto

Function g is one-one but not onto.

Hence the result is not true.

Question 2. Check the injectivity and surjectivity of the following functions:

1. f: N → N given by f(x) = x²
2. f: Z → Z given by f(x) – x²
3. f: R → R given by f(x) = x²
4. f: N → N given by f(x) = x³
5. f: Z → Z given by f(x) = x³

Solution:

1.f: N → N is given by, f(x) = x²

Let x₁ x₂ ∈ N, such that if f(x₂) = f(x²) x₁² =x₂²

⇒ (x₁ – X₂) (x₁ + x₂) = 0 ⇒ x₁ – x₂ = 0 ⇒ x₁ = x₂ (∴ x₁ + x₂ ≠0)

∴ f is injective.

Let y ∈ N (codomain)

Put y = f(x) = x² ⇒ x = √y <∉ N, ∀y ∈N

Every element of the codomain does not have pre-images in the domain.

Range 54 Co-domain

For eg. range of f = {1,4, 9…,} ≠ co-domain of f

∴ f is not surjective.

Hence, function f is injective but not surjective.

2. f: Z → Z is given by, f(x) = x₂ Let x₁ x₂ ∉ Z, such that

If f(X₁) = f(x₂) ⇒ x²₁ = X²₂

⇒ (X₁ – X₂) (x₁ + x₂) = 0

⇒ x₁ + x₂ = 0 or x₁ = x₂ ⇒ x₁ + x₂ = 0 or x₁ = – x₂

∴ The function does not have a unique solution

f is not injective Let y ∈ Z (co-domain)

Put y = f(x) = x² ⇒ x = √y ∉ Z, ∀ y ∈ Z

Every element of the co-domain does not have pre-images in the domain.

Range ≠ Co-domain

For example: f(-1) = f(1) = I, but – 1 ≠1,

f is not injective.

Since the range of f = {0, 1, 4, 9 } ≠ co-domain of f.

∴ f is not surjective.

Hence, function f is neither injective nor surjective.

3. f: R → R is given by f(x) = x²

Let x₁ x₂ ∈ R, such that if f(x,) = f(x₂) ⇒ x²₁ = x²₂ ⇒ (x₁ – x₂) (x₁ + x₂) = 0

x₁ – x₂ = 0 and x₁ = x₂

x₁ + x₂ = 0 and x₁ = – x₂

The function does not have a unique solution

∴ f is not injective.

Let y ∉ R (co-domain)

Put y = f(x) = x”⇒ x = ,√y<∉ R, ∀ y ∈ R

Every element of the co-domain does not have an image in the domain

Range ≠ co-domain

For example ; f(-1) – f(l) = 1, but – 1 ≠ 1,

∴ f Is not injective.

Since, the range of f ≠ co-domain of f

∴ f is not surjective.

Hence, function f is neither injective nor surjective.

4. f: N → N is given by, f(x) = x³

Let x₁ x₂∈N (domain) such that if f(x₁) = f(x₂)

⇒ \( x_1^3=x_2^3 \Rightarrow\left(x_1-x_2\right)\left(x_1^2+x_1 x_2+x_2^2\right)\)=0

⇒ \( x_1-x_2=0 \Rightarrow x_1=x_2 ( x_1^2+x_1 x_2+x_2^2 \neq 0)\)

∴ f is injective.

Let y ∈ N (co-domain)

Put y = f(x) = x³ = (y)^1/3 ∉ N, ∀y ∈ N

Every element of the co-domain does not have pre-images in the domain.

Range ≠ co-domain

Range of f = {1, 8, 27 } ≠ co-domain of f

∴ f is not surjective.

Hence, function f is injective but not surjective.

5. f: Z → Z is given by, f(x) = x³

Let x₁ x₂ ∈ Z (domain) such that

if  \(f\left(x_1\right)=f\left(x_2\right) \Rightarrow x_1^3=x_2^3 \)

⇒ \(\left(x_1-x_2\right)\left(x_1^2+x_1 x_2+x_2^2\right)=0 \Rightarrow\left(x_1-x_2\right)\left[\left(x_1+\frac{x_2}{2}\right)^2+\frac{3}{4} x_2^2\right]\)=0

⇒ \(x_1=x_2\left(\left(x_1+\frac{x_2}{2}\right)^2+\frac{3}{4} x_2^2 \neq 0\right)\)

∴ f is injective.

Let y ∈ Z (co-domain)

Put y = f(x) =x² ⇒ x=(y)^1/3 ∉ Z, ∀y ∉ Z

Every element of the co-domain does not have an image in the domain

Range ≠ co-domain

Range of f = (0, ± 1, ±8, ± 27,…} ≠ co-domain of f.

∴ f is not surjective.

Hence, the function is injective but not surjective.

Question 3. Prove that the Greatest Integer Function f: R → R given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.

Solution:

f: R → R is given by, f(x) = [x]

It is seen that f(1.2) = [1.2] = 1, f(1.9) = [1.9] = 1.

f(1.2)-f(1.9), but 1.2 ≠ 1.9.

∴ f is not one-one.

Range of f = I

⇒ Range of f ≠ co-domain of f.

f is not onto.

Hence, the greatest integer function is neither one-one nor onto.

Question 4. Show that the Modulus Function f: R → R given by f(x) — |x|, is neither one-one nor onto, where ]xj is x if x is positive or 0 and j x | is – x, if x is negative,

Solution:

f: R → R is given by, f(x) = | x | = { x,  if  \(x \geq 0\)  -x,  if  x<0

It is seen that f(-1) = |-1| = 1, f(1) = | 1 | = 1.

f(-1) = f(1), but -1 ≠ 1

∴ f is not one-one.

Range of f = R+ ∪ {O} ⇒ range of f ≠ co-domain of f,

∴ f is not onto.

Hence, the modulus function is neither one-one nor onto.

Question 5. Show that the Signum Function f: R → R is given by, \(\mathrm{f}(\mathrm{x})= \begin{cases}1, & \text { if } \mathrm{x}>0 \\ 0, & \text { if } x=0 \\ -1 & \text { if } x<0\end{cases}\), is neither one-one nor onto.

Solution:

f: R → R is given by, \(\mathrm{f}(\mathrm{x})= \begin{cases}1, & \text { if } \mathrm{x}>0 \\ 0, & \text { if } x=0 \\ -1 & \text { if } x<0\end{cases}\)

∴ Y f(x) – 1, ∀ x ∈ (0, ∞) and f(x) = – 1, ∀ x ∈(-∞, 0)

∴ f is not one-one.

Range of f= {0, ± 1}

Range of f ≠ co-domain off.

So, f is not onto.

Hence, the signum function is neither one-on-one nor onto,

Question 6. Let A = (1, 2, 3), B = {4, 5, 6, 7} and let f = ((1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.

Solution:

It is given that A = {1, 2, 3}, B = (4, 5, 6, 7}.

f: A → B is defined as f = {(1,4), (2, 5), (3, 6)}.

f(1) = 4, f(2) = 5, f(3) = 6

Since different elements of A have different images in B

Hence, function f is one-one.

Question 7. In each of the following cases, state whether the function is one-one, onto, or bijective. Justify your answer.

1. f: R → R defined by f(x) = 3 – 4x
2. f: R→ R defined by f(x) = 1 + x₂

Solution:

1. f: R →  R defined by f(x) = 3 – 4x.

Let x₁ x₂ ∈ R such that f(x,)= f(x²)

⇒ 3 – 4x₁ = 3 – 4x₂

⇒ – 4x₁ = – 4x₂ ⇒ x₁ = x₂

∴ f is one-one.

Let y ∈ R (co-domain) put y = f(x) ⇒ y = 3 – 4x

x=\(\frac{3-y}{4} \in\) R (domain),  \(f\left(\frac{3-y}{4}\right)=3-4\left(\frac{3-y}{4}\right)=y, \forall y \in\) R (co-domain)

∴ f is onto.

Since f is one-one and onto.

Hence, f is bijective.

2. f:R→ R is defined as, f(x) = 1 + x².

Let x₁ x₂ ∈ R such that f(x₁) = f(x₂)

1 + x²₁ – 1 + x²₂ ⇒ x²₁ = X²₂ ⇒ x₁ – ± x₂

f(1) = 2, f(-1) = 2

⇒ f(l) = f(-l) but 1 ≠ – 1

∴ f is not one-one.

Here range of f = [1, ∞)

∴  Range of f ≠ co-domain of f.

∴ f is not onto.

Hence, f is neither one-one nor onto.

Question 8. Let A and B be sets. Show that f: AxB → B x A such that f(a, b) = (b, a) is a bijective function.

Solution:

f: AxB → BxA is defined as f(a, b) = (b, a).

Let (a₁b₁), (a₂ b₂) ∈ A x B such that if f(a,b,) = f(a₂ b₂)

⇒ (b₁ a₁) = (b₂ a₂) ⇒ b₁= b₂ and a₁ = a₂ ⇒ (a₁ b₁) = (a₁ b₂).

So, f is one-one.

Now, let (b, a) ∈ B x A ⇒ (a, b) ∈ A x B

i.e. ∀ (b, a) ∈ B x A, ∃ (a, b) ∈ A x B such that f(a, b) = (b, a). (Definition of f)

So, f is onto, Hence, f is bijective.

Question 9. Let f: N \(\rightarrow N \text { be defined by } f(n)=\left\{\begin{array}{ll} \frac{n+1}{2}, & \text { if } n \text { is odd } \\ \frac{n}{2}, & \text { if } n \text { is even } \end{array} \text {, for all } n \in N\right.\)
State whether the function f is objective. Justify your answer

Solution:

f(1)=\(\frac{1+1}{2}=1, f(2)=\frac{2}{2}=1 \Rightarrow f(1)=f(2) \text { but } 1 \neq 2\)

f is not one-on-one.

∴ Hence, f is not bijective.

Question 10. Let \(\mathrm{A}=\mathrm{R}-\{3\}\) and \(\mathrm{B}=\mathrm{R}-\{1\}\). Consider the function f: \(\mathrm{A} \rightarrow \mathrm{B}\) defined by \(\mathrm{f}(\mathrm{x})=\left(\frac{\mathrm{x}-2}{\mathrm{x}-3}\right)\) Is f one-one and onto? Justify your answer.

Solution:

Let \(x_1, x_2 \in\) A such that \(f\left(x_1\right)=f\left(x_2\right)\)

⇒ \(\frac{x_1-2}{x_1-3}=\frac{x_2-2}{x_2-3} \Rightarrow\left(x_1-2\right)\left(x_2-3\right)=\left(x_2-2\right)\left(x_1-3\right) \)

⇒  \(x_1 x_2-3 x_1-2 x_2+6=x_1 x_2-3 x_2-2 x_1+6\)

⇒  \(-3 x_1-2 x_2=-3 x_2-2 x_1 \)

⇒  \(3 x_1-2 x_1=3 x_2-2 x_2 \)

⇒  \(x_1=x_2\)

∴ f is one-one.

\(\text { Let } y=f(x) \forall y \in\) B

y=\(\frac{x-2}{x-3} \Rightarrow \)x y-3 y=x-2

x y-x=3 y-2

x(y-1)=3 y-2 \(\Rightarrow x=\frac{3 y-2}{y-1}\)

every element of B has pre-images in A.

Range = co-domain

∴  f is onto.

Hence, function f is one-one and onto.

Question 11. Let f: R → R be defined as f(x) = x⁴. Choose the correct answer.

1.  f is one – one onto
2.  f is many-one onto
3.  f is one-one but not onto
4.  f is neither one-on-one nor onto

Solution: 4.

f: R → R is defined as f(x) = x⁴

f( 1) = 1, f(-1) = 1 => f( 1) = f(-1) but 1 1,

So. f is not one-one

Again, Range of f = [0, <=o)

range of f c co-domain of f.

∴ So, f is not onto.

Hence, function f is neither one-one nor onto.

Question 12. Let f: R→ R be defined as fix) = 3x. Choose the correct answer.

1.  f is one-one onto
2.  f is many-one onto
3. f is one-one but not onto
4. f is neither one-on-one nor onto

Solution: 1.

Let \(\mathrm{x}_1 \mathrm{x}_2 \in \mathrm{R}\) such that \(\mathrm{f}\left(\mathrm{x}_1\right)=\mathrm{f}\left(\mathrm{x}_2\right) \Rightarrow 3 \mathrm{x}_1=3 \mathrm{x}_2 \Rightarrow \mathrm{x}_1=\mathrm{x}_2\).

So f is one – one.

Let y=f(x) \(\forall y \in\) R

y=3 x \(\Rightarrow x=\frac{y}{3} \in\) R

Range ≠ Co-domain.

So f is onto Hence, function f is one-one and onto.

Relations And Functions Miscellaneous Exercise

Question 1. Show that function f: \(\{\mathrm{x} \in \mathrm{R}:-1<\mathrm{x}<1\}\) defined by \(\mathrm{f}(\mathrm{x})=\frac{\mathrm{x}}{1+|\mathrm{x}|}, \mathrm{x} \in \mathrm{R}\) Is one-one and onto function.

Solution:

For one-one function :

Case-1: when \(\mathrm{x}_1, \mathrm{x}_2>0\)

Let f\(\left(x_1\right)=f\left(x_2\right) \Rightarrow \frac{x_1}{1+x_1}=\frac{x_2}{1+x_2} \Rightarrow x_1+x_1 x_2=x_2+x_1 x_2 \Rightarrow x_1=x_2\)

Case-2: when \(\mathrm{x}_1, \mathrm{x}_2<0\)

Let f\(\left(x_1\right)=f\left(x_2\right) \Rightarrow \frac{x_1}{1-x_1}=\frac{x_2}{1-x_2} \Rightarrow x_1-x_1 x_2=x_2-x_1 x_1 \Rightarrow x_1=x_2\)

Case-3: when \(x_1>0, x_2<0\)

Let f\(\left(x_1\right)=f\left(x_2\right) \Rightarrow \frac{x_1}{1+x_1}=\frac{x_2}{1-x_2} \Rightarrow x_1-x_1 x_2=x_2+x_1 x_2 = 0\)

which is not possible \((\mathrm{x}_1>0, \mathrm{x}_2<0)\)

⇒ \(\mathrm{x}_1 \neq \mathrm{x}_2 \Rightarrow \mathrm{f}\left(\mathrm{x}_1\right) \neq \mathrm{f}\left(\mathrm{x}_2\right)\)

∴ f is one-one

For onto function :

Case-I

When x \(\geq\) 0

Let y=f(x)

y=\(\frac{x}{1+x}\)

y+x y=x

or y=x(1-y)

x=\(\frac{y}{1-y}\)

or x=-\(\frac{y}{(y-1)} \geq 0\)

⇒ \(\frac{y}{y-1} \leq 0\)

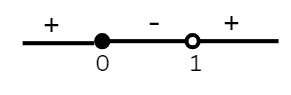
y \(\in\)[0,1)

Case-2

When \(\mathrm{x}<0\)

Let y=f(x)

y=\(\frac{x}{1-x}\)

y-x y=x

or y=x+x y

x=\(\frac{y}{1+y} \)

x=\(\frac{y}{1+y}<0\)

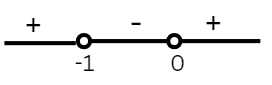
y \(\in\)(-1,0)

From Case 1 and Case 2, y ∈  [0,1) ∪ (-1,0)

Range = (-1,1) = Co-domain

∴ So, f is onto.

Hence, f is one-one and onto function.

Question 2. Show that the function f: R ⇒ R given by f(x) = x³ is injective.

Solution:

f: \(\rightarrow \)R is given as f(x)=\(x^3\).

Let \(x_1, x_2 \in\) R such that if f\(\left(x_1\right)=f\left(x_2\right)\)

⇒ \(x_1^3=x_2^3 \Rightarrow\left(x_1-x_2\right)\left(x_1^2+x_2^2+x_1 x_2\right)\)=0

⇒ \(\left(x_1-x_2\right)\left[\left(x_1+\frac{x_2}{2}\right)^2+\frac{3}{4} x_2^2\right]\)=0

⇒ \(x_1-x_2=0\left[\left(x_1+\frac{x_2}{2}\right)^2+\frac{3}{4} x_2^2 \neq 0\right]\)

⇒ \(x_1=x_2 \)

∴ f is injective

Question 3. Given a nonempty set X, consider P(X) which is the set of all subsets of X. Define the relation R in P(X) as follows:

For subsets A, and B in P(X), ARB if and only if Ac B. Is R an equivalence relation on P(X)? Justify your answer:

Solution:

Since every set is a subset of itself, ARA, ∀ A ∈ P(X).

∴ R is reflexive.

Let ARB ⇒ A ⊂ B. ≠ B ⊄ A.

For Example: if A = {1,2} and B = {1, 2, 3}, then A ⊂ B but B ⊄ A

∴ R is not symmetric.

Since R is not symmetric.

Hence, R is not an equivalence relation on P(X).

Question 4. Find the number of all onto functions from the set {1, 2, 3,…, n) to itself.

Solution:

Since f is onto function, so all elements of set {1, 2,…n} have unique.

pre-image in set (1,2,…n}

So. the total number of onto functions = n x (n-1) x {n — 2)x …x 2 x 1= n!

Question 5. Let \(\mathrm{A}=\{-1,0,1,2\}, \mathrm{B}=\{-4,-2,0,2\}\) and \(\mathrm{f}, \mathrm{g}: \mathrm{A} \rightarrow \mathrm{B}\) be functions defined by \(f(x)=x^2-x, x \in A\) and \(g(x)=2\left|x-\frac{1}{2}\right|-1, x \in\) A. Are f and g equal? Justify your answer.

Solution:

Given A={-1,0,1,2}, B={-4,-2,0,2}.

Also, f: A \(\rightarrow B, f(x)=x^2-x, \forall x \in A\)

⇒ \(\mathrm{g}: \mathrm{A} \rightarrow \mathrm{B}, \mathrm{g}(\mathrm{x})=2\left|\mathrm{x}-\frac{1}{2}\right|-1, \forall \mathrm{x} \in \mathrm{A}\)

It is observed that :

f(-1)=(-1)^2-(-1)=1+1=2

⇒ \(g(-1)=2\left|(-1)-\frac{1}{2}\right|-1=2\left(\frac{3}{2}\right)-1=3-1=2 \Rightarrow f(-1)=g(-1)\)

⇒ \(f(0)=(0)^2-0=0 ; g(0)=2\left|0-\frac{1}{2}\right|-1=2\left(\frac{1}{2}\right)-1=1-1=0 \Rightarrow f(0)=g(0)\)

⇒ \(f(1)=(1)^2-1=1-1=0 ; g(1)=2\left|1-\frac{1}{2}\right|-1=2\left(\frac{1}{2}\right)-1=0 \Rightarrow f(1)=g(1) \)

⇒ \(f(2)=2^2-2=4-2=2 ; g(2)=2\left|2-\frac{1}{2}\right|-1=2\left(\frac{3}{2}\right)-1=3-1=2 \Rightarrow f(2)=g(2)\)

Thus \(\forall \mathrm{a} \in \mathrm{A}, \mathrm{f}(\mathrm{a})=\mathrm{g}(\mathrm{a})\)

f and g are equal functions.

Question 6. Let A = {1, 2, 3). The number of relations containing (1,2) and (1,3) which are reflexive and symmetric but not transitive is

1. 1
2. 2
3. 3
4. 4

Solution:

1. The given set is A = {1,2, 3},

The smallest relation containing (1, 2) and (1, 3) which is reflexive and symmetric, but not transitive is given by:

R = {(1, 1), (2, 2), (3, 3), (1,2), (1,3), (2, 1), (3, 1)}

Since (1, 1), (2, 2), (3, 3) ∈ R.

∴ So R is reflexive

Since (1, 2), (2. 1) ∉ R and (1, 3), (3, 1) ∉ R.

So R is symmetric Since (3, 1), (1, 2) ∈ R, but (3, 2) ∉ R.

∴ So R is not transitive

Now, if we add ordered pairs (3, 2) and (2, 3) to relation R, then relation R will become transitive.

Hence, the total number of desired relations is one.

Question 7. Let A = {1, 2, 3). The number of equivalence relations containing (1,2) is

1. 1
2. 2
3.  3
4.  4

Solution: 2.

It is given that A = -(1,2,3}.

The smallest equivalence relation containing (1, 2) is given by,

R = {(I,1), (2, 2), (3, 3), (1,2), (2,1)}

Now, we are left with only four pairs i,e., (2, 3), (3, 2), (1, 3), and (3, 1).

If we add any one pair [say (2, 3 ) ] to R, then for symmetry we must add (3, 2).

Also, for transitivity, we are required to add (1,3) and (3, 1).

Hence, another equivalence relation R, = {(1, 1), (2, 2), (3, 3), (1,2), (2, 1), (2, 3), (3, 2), (1, 3), (3, 1)}

This shows that the total number of equivalence relations containing (1,2) is two i.e. R₁ and R₂