CBSE Solutions For Class 10 Mathematics Chapter 2 Polynomials

CBSE Solutions For Class 10 Mathematics Chapter 2

Question 1. x²+9x+20

Solution:

Let P(x) = = x²+9x+20

= x²+5x+4x+20

= x(x+5)+4(x+5)

(x+4)(x+5)

P(x)=0

(x+4)(x+5)=0

x+4=0 or x+5=0

x=-4 x=-5

Zeros of P(x) are -4 and -5 \(=\frac{-9}{1}=\frac{- \text { Coefficient of } x}{\text { coefficient of } x^2}\)

Now, Sum of Zeros = -4+(-5) \(\frac{20}{1}=\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)

Question 2. x² – 9

Solution:

Let P(x) = x² = 9 = x²=-32 = (x-3)(x+3)

P(x)=0

(x-3)(x+3)=0

x-3=0 Or x+3=0

x=3 x=-3

Zeros of p(x) are 3 and -3

Now, Sum of Zeros = 3+(-3)=0 = \(\frac{-0}{1}=-\frac{\text { Coefficient of } x}{\text { Coefficient of } x^2}\)

and Product of Zeros = (3)(-3) = −9 = \(\frac{-9}{1}=\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)

Read and Learn More Class 10 Maths

Question 3. Find the quadratic polynomials, the Sum of whose Zeroes is 17 and the product is 60. Hence, find the Zeroes of the polynomial.

Solution:

Let and B be the Zeroes of the polynomial P(X).

Given that X+B=17 and αβ=60

Now, P(x) = x²= (α+β)γ + αβ

= x²= 17x+60

= x²=12x-5x+60

= x(x-12)-5(x-12)

= (x-5)(x-12)

There may be So many different polynomials that satisfy the given Condition. The general equation quadratic polynomial will be k(x2=-17x+60), where k = 0

P(x)=0

(x-5) (x-12) = 0

(x-5)=0 or (x-2)=0

2=5 Or x=12

Zeros are 12 and 5.

Question 4. Find a quadratic polynomial, the Sum of whose Zeros is 7 and the product is -60. Hence, verify the relation between Zeros and Coefficients of the polynomial.

Solution:

Let and B be the Zeros of the polynomial P(x).

Given that α+β=ϒ and αβ = -60

Now, P(x) = x² – (α+β) γ+ αβ

= x²-7x-60

= x²-12x+5x-60

= x(x-2)+5(x-12)

= (x-12)+(x-5)

There may be so many different polynomials which satisfy the given Condition. The general quadratic polynomial will be k (x²-7x-60), where k = 0.

P(x)=0

(x-12) (x+5)=0

(x-12)=0

x=12 or (x+5)=0

x=-5

Zeros are 12 and -5.

Question 5. If the product of Zeroes of the polynomial 30+ 5x+k is 6, find the value of k.

Solution:

Given polynomial = 31751+k

Product of Zeroes = \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)

6= \(\frac{k}{3}\)

= 6×3=k

⇒ k = 18

Question 6. If the Sum of Zeroes of the polynomial x²+2x-12 is 1, find the value of k.

Solution:

Given polynomial = x²+2kx-12

Sum of Zeroes = \(-\frac{\text { Coefficient of } x}{\text { Coefficient of } x^2}\)

1 = \(\frac{-2 k}{1}\)

1 = -2K

⇒ \(k=\frac{-1}{2}\)

Question 7. If x = \(\frac{5}{3}\) and x = \(\frac{-1}{2}\) are the Zeroes of the polynomial ax=7x+b, then find the values of a and b.

Solution: Let P(x) = ax27x+b

⇒ \(x=\frac{5}{3} \text { and } x=\frac{-1}{2}\) are zeroes of p(x)

⇒ \(P\left(\frac{5}{3}\right)=0\)

⇒ \(a\left(\frac{5}{3}\right)^2-7\left(\frac{5}{3}\right)+b\)

⇒ \(\frac{25 a}{9}-\frac{35}{3}+b\)

⇒ \(b=\frac{-25 a}{9}+\frac{35}{3}\)

⇒ \(P\left(\frac{-1}{2}\right)=a\left(\frac{-1}{2}\right)^2-7\left(\frac{-1}{2}\right)+b\)

⇒ \(\frac{a}{4}+\frac{7}{2}+b\)

⇒ \(\frac{a}{4}+\frac{7}{2}-\frac{25 a}{9}+\frac{35}{3}=0\)

⇒ \(\frac{a}{4}-\frac{25 a}{9}=-\frac{7}{2}-\frac{35}{3}\)

⇒ \(\frac{9 a-100 a}{36}=\frac{-21-70}{6}\)

⇒ \(-\frac{91 a}{36}=\frac{-91}{6}\)

⇒ \(\frac{91 a}{6}=91\)

91a = 546

⇒ \(a=\frac{546}{91}\)

a = 6

⇒ \(b=\frac{-25(6)}{9}+\frac{35}{3}\)

⇒ \(b=\frac{-25(6)}{9}+\frac{35}{3}\)

⇒ \(b=\frac{-150+105}{9}\)

⇒ \(b=\frac{-45}{9}\)

b = -5

Question 8. Verify that 1,-2, 4 are Zeros of the Cubic polynomial x³-3x²-6x+8. Also, Verify the relation between Zeroes and Coefficients of the polynomial.

Solution:

Here, P(x) = x³-3x²-6x+8

P(1) = (1)² = 3(1)² – 6(1) +8 = 1-3-6+ 8 = −9+9=0

P(-2) = (2) ³ -3(-2)=6(-2)+8=-8-12+12+8 = 0

P(4) = (4)³-3(4) -6(4) +8 = 64-48-24+8 = 0

1-2 and 4 are Zeroes of P(x).

Now, α+B+= 1-2+4=3 = \(\frac{-3}{1}=-\frac{\text { Coefficient of } x^2}{\text { Coefficient of } x^3}\)

XB+B++√α = (1)(-2)+(-2) (4)+(4)(1) = −2-8+4

= -10+4

⇒\(\frac{-6}{1}=\frac{\text { Coefficient of } x}{\text { Coefficient of } x^3}\)

and LB7 = (1)(-2) (4) =\(-\frac{8}{1}=\frac{8}{1}=\frac{\text { Constant term }}{\text { Coefficient of } x^3}\)

Question 9. Verify that 2-4. and are zeroes of the Cubic polynomial 3x ³ +5x² = 26x+8. Also, verify the relation between Zeroes and Coefficients of the polynomial.

Solution:

Here, P(x)=3x³ +5 x 2 – 26x+8

P(2) = 3(2)3 +5(2)2 = 26(2)+8=24+20-52+8 = 52-52 = 0

P(-4)=3(-4)3 + 5(-4)=26(-4)+8=-(92+80+104+8=-192+192=0

⇒ \(P\left(\frac{1}{3}\right)=3\left(\frac{1}{3}\right)^3+5\left(\frac{1}{3}\right)^2-26\left(\frac{1}{3}\right)+8=\frac{3}{27}+\frac{5}{9}-\frac{26}{3}+8=\frac{3+15-234+216}{27}\)

⇒ \(=\frac{234-234}{27}=0\)

2,-4. and — are Zeroes of P(x),

Now \(\text { , } \alpha+\beta+\gamma=2-4+\frac{1}{3}=-2+\frac{1}{3}=\frac{-6+1}{3}=-\frac{5}{3}=\frac{5}{3}=-\frac{\text { Coefficient of } x^2}{\text { Coefficient of } x^3}\)

⇒ \(\alpha \beta+\beta \gamma+\gamma \alpha=(2)(-4)+(-4)\left(\frac{1}{3}\right)+\left(\frac{1}{3}\right)(2)=-8-\frac{4}{3}+\frac{2}{3}=\frac{-28+2}{3}=\frac{-26}{3}\)

⇒ \(=\frac{- \text { Coefficient of } x^2}{\text { coefficient of } x^3}\)

and \(\alpha_\beta \beta=(2)(-4)\left(\frac{1}{3}\right)=-\frac{-8}{3}=\frac{8}{3}=\frac{\text { Constant term }}{\text { Coefficient of } x^3}\)

Question 10. Find a Cubic polynomial whose Zeroes are 5, 6, and -4.

Solution:

Let α= 5, β=6 and γ=-4

α+β+ γ = 5+6-4 =) ||- 4 = 7

αB+ βγ + γα = 5(6)+6(-4)+(-4) (5)

= 30-24-20

= 30-44

= -14

XB = 5(6)(u)

= -120

Cubic Polynomial = x³-(x+β++) x² + (αβ+ βγ + γα) x-px

= x² – (7) x2 + (-14)x-(-120)

= x³-7x² = 14x+120

Question 11. Find a Cubic polynomial whose Zeroes are 11 and -1.

Solution:

let α= \(\frac{1}{2},\),B = 1 and 2 =-1

⇒ \(\alpha+\beta+\gamma=\frac{1}{2}+1-1=\frac{1}{2}\)

⇒ \(\alpha_\beta+\beta^1+\gamma \alpha=\frac{1}{2}(1)+(1)(-1)+(-1)\left(\frac{1}{2}\right) \Rightarrow \frac{1}{2}-1-\frac{1}{2} \Rightarrow-1\)

⇒ \(\alpha \beta \gamma=\frac{1}{2}(1)(-1) \Rightarrow \frac{-1}{2}\)

Cubic polynomial = x³= (α+β+γ) x2 + (αβ+ βγ + γα)x-αßγ

⇒ \(x^3-\frac{1}{2} x^2+(-1) x-\left(-\frac{1}{3}\right)\)

⇒ \(x^3-\frac{1}{2} x^2-x+\frac{1}{2}\)

⇒ \(2 x^3-x^2-2 x+1\)

Question 12. Find the quotient and remainder in each of the following and verify the division algorithm:

1. P(x) = x²=14x²+2x-1 is divided by g(x)=x+2

Solution:

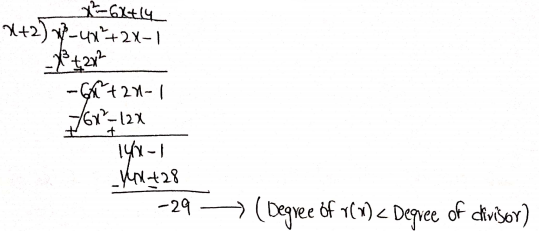
Now, quotient = x2=6x+14, remainder = -29

dividend = x³-4x²+2x-1 and divisor = x+ 2

and quotient x divisor + remainder = (x²-6x+(4)(x+2)-29

= x²-6x²+14x+2x²=1271+28-29

= x²-4x² +2x-1

= dividend

2. P(x) = x² + 2x²= x + 1 is divided by g(x) = x²+1

Solution:

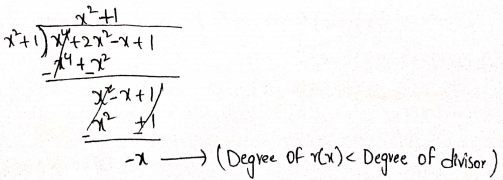
Now, quotient = x²+1, remainder = -x, dividend = x² + 2x = x +1 and

divisor = x+1

and quotient divisor + remainder = (x² + 1)(x² + 1) – α = ) x + x2 + x² + 1-x

x 4 + 2x = x + 1 =) dividend

Question 13. Actual division shows that x+2 is a factor of x³ + 4x²+3x-2.

Solution:

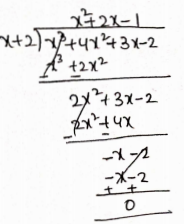
Question 14. If I am a zero of the polynomial x²-4x²=7x+10, find its other two Zeroes

Solution:

let P(x)=x³=_472-70+10

x= 1 is a zero of P(x)

(x-1) is a factor of P(x)

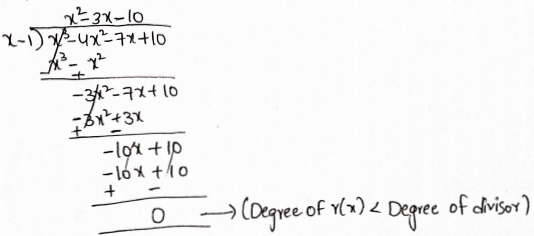
P(x) = x3- 4x²-7x+ 10 =) (x-1) (x=3x-10)

(x-1) (x²+2x-5x-10)

(x-1) ((x(x+2)-5(x+2))

(x-1)(x+2)(x-5)

Now, P(x)=0

⇒ (x-1)(x+2)(x-5)=0

⇒ α-1=0 or x+2=0 or x-5=0

x=1 or x=-2 or x=5

Hence, other Zeroes are -2 and 5

Question 15. If Land -2 are two Zeroes of the polynomial x⁴+x³=11x=9x+18, find the other two Zeroes.

Solution:

Let P(x) = x² + x² – 1172=9x+18

x=1, x=-2 is a zero of p(x)

(x-1) (x+2) is a factor of P(x)

x²+2x-x-2 =) x²+x-2 is a factor of P(x)

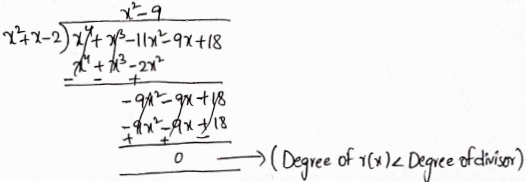
p(x0 = x4 = x3 – 11×2 – 9x + 18 = (x-1)(x+2)(x2-9)

= (x-1)(x+2)(x²-32)

= (x-1)(x+2)(x+3)(x-3)

Now P(x)

(x-1)(x+2)(x+3)(x-3)=0

= (x-1)(x+2)(x+3)(x-3)

⇒ x-1=0 x+2=0

⇒ x+3=0 X-3=0

⇒ x=1 x=-2 x=-3 X=3

Hence, other Zeroes are 3 and -3.

Question 16. Find all Zeroes of x + x3-23x=-3x+60, if it is given that two of its Zeroes are √3 and -√3.

Solution:

Let P(x) = x2+x3-28x=-3x+60

√3 and -√3 are Zeroes of P(x).

(x−√3)(x+√3) = x2= 3 is a factor of P(x).

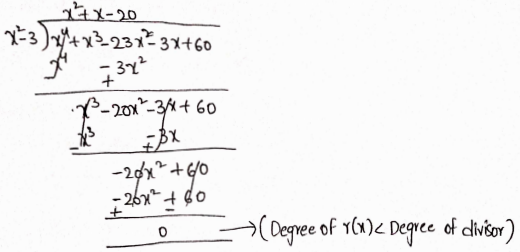
P(x) = x²+x³-x²=3x+60 = (x²=3)(x²+11-20)

= (x²-3) [x²+5x-4x-20]

=(x²-3)(x(x+5)-4(x+5))

= (x²-3)(x-4)(x+5)

The other Zeroes are given by

x-4=0 or x+5=0

⇒ x=4 Οr x=-5

Hence, other Zeroes are 4 and -5.

Question 17. Find Zeroes of the polynomial f(x) = x² – 13x² + 32x – 60, if it is given that the Product of its two Zeroes is 10.

Solution: Let α, B, be Zeroes of the given polynomial p(x), Such that &p=10-)(1)

⇒ \(\alpha+\beta+\gamma=\frac{-(-13)}{1}=13 \longrightarrow(2)\)

⇒ \(\alpha \beta+\beta 1+\alpha \gamma=\frac{32}{1}=32 \longrightarrow(3)\)

⇒ \(\alpha \beta \gamma=-\frac{(-60)}{1}=60 \longrightarrow(4)\)

From (1) and (4)

10s=60

⇒ \(\gamma=\frac{60}{10} \Rightarrow \gamma=6 \rightarrow(5)\)

Put 7=6 in (2), we get α+3 +6 = 13

α+B=7

Now, (α-B)² = (x+3)=4xß

= (7)=4(10)

= 49-40

= 9

α-B = ± 3 —– (6)

Solving (5) and (6), we get

α=2,B=5 or α=2, B=5 and 1=6.

So, Zeroes are 2,5 and 6.

Question 18. What must be added to P(x) = 4x² – 5x = 39x = 46x = -2, so that the resulting Polynomial is divisible by g(x) = 4x² + 7x + 2 ?

Solution:

P(x) = 4×4 -5x³-39x²– 46x-2

9(x)= 4x²+7x+2