Application of Integrals Class 12 Maths Important Questions Chapter 8

Applications Of Integrals Exercise 8.1

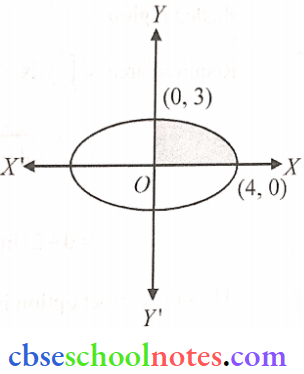
Question 1. Find the area of the region bounded by the ellipse \(\frac{x^2}{16}+\frac{y^2}{9}=1\)
Solution:

The given curve is an ellipse with center at (0, 0) and symmetrical about both the X-axis and Y-axis (the power of x and y both are even)

Area bounded by the ellipse = 4 x (Area of the shaded region in the first, quadrant only)

(∵ By symmetry)

= \(4 \times \int_a^b y d x=4 \int_0^4 y d x=4 \int_0^4 \frac{3}{4} \sqrt{16-x^2} d x\)

(because \(\frac{x^2}{16}+\frac{y^2}{9}=1\) therefore \(y=\frac{3}{4} \sqrt{16-x^2}\))

= \(3 \int_0^4 \sqrt{4^2-x^2} d x=3\left[\frac{x}{2} \sqrt{4^2-x^2}+\frac{4^2}{2} \sin ^{-1}\left(\frac{x}{4}\right)\right]_0^4\)

(because \(\int \sqrt{a^2-x^2} d x=\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1}\left(\frac{x}{a}\right)+C\))

= \(3\left[2 \sqrt{16-16}+8 \sin ^{-1}(1)-0-8 \sin ^{-1}(0)\right]\)

= \(3\left[0+8 \sin ^{-1}(1)-0\right]=3 \times 8 \times\left(\frac{\pi}{2}\right)=12 \pi \) (sq. units.)

Therefore, the area bounded by the ellipse is \(12 \pi\) sq. units.

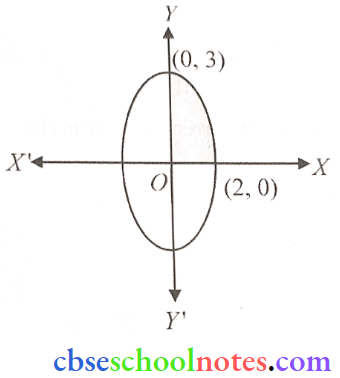
Question 2. Find the area of the region bounded by the ellipse \(\frac{x^2}{4}+\frac{y^2}{9}=1\).
Solution:

The given curve is an ellipse with center at (0, 0) and symmetrical about both the X-axis and Y-axis. The area bounded by the ellipse

= 4x (Area of the shaded region in the first quadrant only) (7 By symmetry)

= \(4 \times \int_a^b y d x\)

= \(4 \int_0^2 y d x=4 \int_0^2 \frac{3}{2} \sqrt{4-x^2} d x\)

(because \(\frac{x^2}{4}+\frac{y^2}{9}=1\), therefore \(y=\frac{3}{2} \sqrt{4-x^2}\))

= \(6 \int_0^2 \sqrt{2^2-x^2} d x=6\left[\frac{x}{2} \sqrt{4-x^2}+\frac{2^2}{2} \sin ^{-1}\left(\frac{x}{2}\right)\right]_0^2\)

(because \(\int \sqrt{a^2-x^2} d x=\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1}\left(\frac{x}{a}\right)+C\))

= \(6\left\{0+2 \sin ^{-1}(1)-0\right\}=6 \times 2 \times\left(\frac{\pi}{2}\right)=6 \pi\) (sq. units)

Read and Learn More Class 12 Maths Chapter Wise with Solutions

Choose The Correct Answer

Question 3. The area lying in the first quadrant and bounded by the circle x²+y² =4 and the lines x = 0 and x = 2 is.

1. \(\pi\)
2. \(\frac{\pi}{2}\)
3. \(\frac{\pi}{3}\)
4. \(\frac{\pi}{4}\)

Solution: 1. \(\pi\)

The area bounded by the circle and the lines x = 0 and x = 2, in the first quadrant is represented by a shaded region.

Required area = \(\int_0^2 y d x=\int_0^2 \sqrt{4-x^2} d x\)

= \(\left[\frac{x}{2} \sqrt{4-x^2}+\frac{4}{2} \sin ^{-1}\left(\frac{x}{2}\right)\right]_0^2\)

= \(0+2 \sin ^{-1}(1)-0=2 \times \frac{\pi}{2}=\pi \text { sq units. }\)

Thus the correct option is (1)

Question 4. Area of the region bounded by the curve y² = dx. Y-axis and the line y = 3 is.

1. 2
2. 9/4
3. 9/3
4. 9/2

Solution: 2. 9/4

The area bounded by the curve, y² = 4x, Y-axis, and y = 3 is represented in the figure by a shaded region.

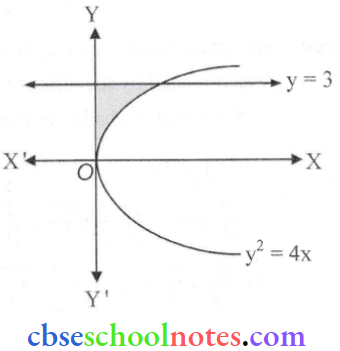
Required area = \(\int_0^3 x d y\)

= \(\int_0^3 \frac{y^2}{4} d y=\frac{1}{4}\left[\frac{y^3}{3}\right]_0^3=\frac{1}{12}\left(3^3-0\right)=\frac{1}{12}(27)=\frac{9}{4}\) (sq units.)

Applications Of Integrals Miscellaneous Exercise

Question 1. Find the area under given curves and given lines.

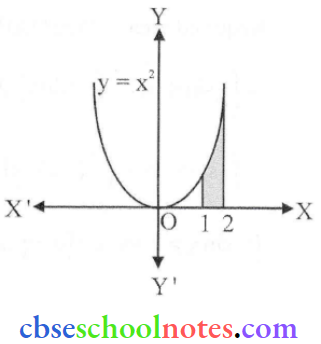
1. y = x²; x = 1, x = 2 and X-axis
2. y = x⁴; x = 1, x = 5 and X-axis

Solution:

1. The given curve y = x² represents an upward parabola with vertex (0, 0) and axis along the Y-axis.

∴ Required area (Shown in shaded region)

= Area under the curve y = x² and between x = l1,x = 2

= \(\int_1^2 y d x=\int_1^2 x^2 d x=\left[\frac{x^3}{3}\right]_1^2=\frac{1}{3}\left[2^3-1^3\right]=\frac{8}{3}-\frac{1}{3}=\frac{7}{3}\) (sq. units.)

2. Given y = x⁴

Here, x is even so the curve is symmetrical about Y -the axis and passes through the origin (0, 0)

∴ Required area = Area under the curve y = x⁴ and between x = 1 , x = 5

Question 2. Sketch the graph of y=|x+3| and evaluate \(\int_{-6}^0|x+3| d x\).
Solution:

y=|x+3|= \(\begin{cases}(x+3) & \text { for } x \geq-3 \\ -(x+3) & \text { for } x<-3\end{cases}\)

Now, \(\int_{-6}^0|x+3| d x\)

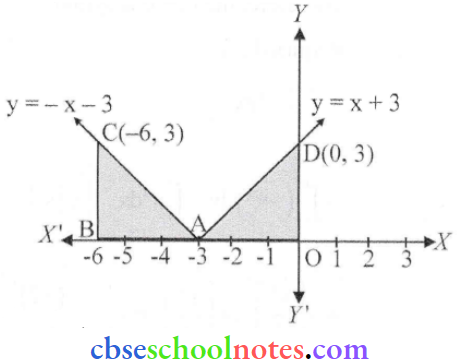
Required area = Area (ΔABC)+ Area(ΔOAD)

= \(\int_{-6}^{-3}(-\mathrm{x}-3) \mathrm{dx}+\int_{-3}^0(\mathrm{x}+3) \mathrm{dx}=\left[\frac{-\mathrm{x}^2}{2}-3 \mathrm{x}\right]_{-6}^{-3}+\left[\frac{\mathrm{x}^2}{2}+3 \mathrm{x}\right]_{-7}^0\)

= \(\left[\left(\frac{-(-3)^2}{2}-3 \times(-3)\right)-\left(\frac{-(-6)^2}{2}-3 \times(-6)\right)\right]+\left[0-\left(\frac{(-3)^2}{2}+3 \times(-3)\right)\right]\)

= \(\left[\left(\frac{-9}{2}+9\right)-(-18+18)\right]+\left[\frac{9}{2}\right]=\frac{9}{2}+\frac{9}{2}=9\) (Sq. units)

Question 3. Find the area bounded by the curve y = sin x between x = 0 and x = 2π
Solution:

The area of the region bounded by y = sin x, x = 0, and x = 2π is shown

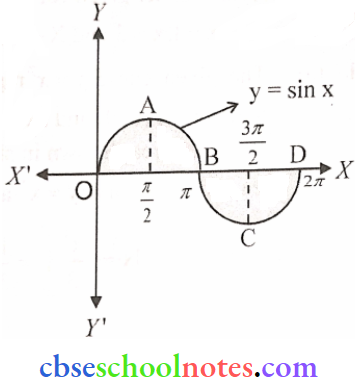
Required area = Area OABO + Area BCDB

= \(\int_0^\pi|\sin x| \mathrm{dx}+\int_\pi^{2 \pi}|\sin \mathrm{x}| \mathrm{dx}\)

= \(\int_0^\pi \sin \mathrm{x} x+\int_\pi^{2 \pi}(-\sin \mathrm{x}) \mathrm{dx}\)

(because \(\sin \mathrm{x} \geq 0\) for \(\mathrm{x} \in[0, \pi]\) and \(\sin \mathrm{x} \leq 0\) for \(\mathrm{x} \in[\pi, 2 \pi]\)

= \([-\cos \mathrm{x}]_0^\pi+[\cos \mathrm{x}]_\pi^{2 \pi}=-\cos \pi+\cos 0+\cos 2 \pi-\cos \pi=-(-1)+1+1-(-1)=4\) sq units.

Choose The Correct Answer

Question 4. The area bounded by the curve y = x³, the X-axis, and coordinates x = -2 and x = 1 is

1. -9
2. -15/4
3. 15/4
4. 17/4

Solution: 4. 17/4

Given curve is y = x³

On putting x = – x and y = — y we get y = x³

Therefore, the curve is symmetrical in the opposite quadrant and passes through (0, 0).

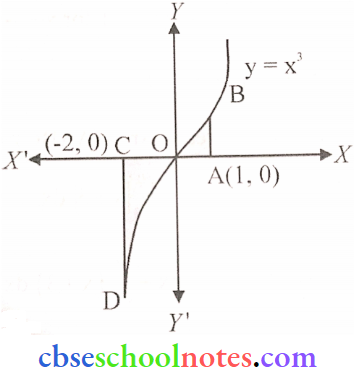
∴ Required area

= \(\int_{-2}^1\left|\mathrm{x}^3\right| \mathrm{dx}\)

= \(\int_{-2}^0\left(-\mathrm{x}^3\right) \mathrm{dx}+\int_0^1 \mathrm{x}^3 \mathrm{dx}\) (because \(\left|\mathrm{x}^3\right|\))

= \(\int_{-2}^0\left(-x^3\right) \mathrm{d} x+\int_0^1 x^3 \mathrm{~d} x\)

(because \(\left|x^3\right|=\left\{\begin{array}{c}
x^3, \text { if } x \geq 0 \\
-x^3, \text { if } x<0
\end{array}\right\}\))

= \(-\left[\frac{x^4}{4}\right]_{-2}^0+\left[\frac{x^4}{4}\right]_0^1=-\left[0-\frac{(-2)^4}{4}\right]+\left[\frac{1}{4}-0\right]\)

= \(-(-4)+\left(\frac{1}{4}\right)=\frac{17}{4}\) sq. units.

So, the correct option is (4).

Question 5. The area bounded by the curve y = x|x|, X-axis, and the coordinates x = -1 and x = 1 is given by

1. 0
2. 1/3
3. 2/3
4. 4/3

Solution: 3. 2/3

Given y \(=x|x|=\left\{\begin{array}{l}
x^2, x \geq 0 \\
-x^2, x<0
\end{array}\right.\)

Required area

= 2 (Area under the curve y = x² between x = 0, x = 1)

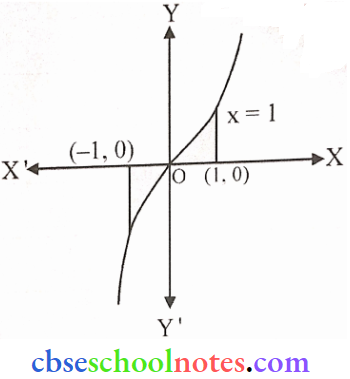
The curve is symmetrical in the opposite; quadrant

= \(2 \int_0^1 x|x|=2 \int_0^1 x^2 d x\)

= \(2\left[\frac{x^3}{3}\right]_0^1=\frac{2}{3}\left(1^3-0^3\right)\)

= \(\frac{2}{3}\) sq. units

So, the correct option is (3).